题目内容
 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.(1)在AC上找一点P,使△BPE的周长最小;
(2)求出△BPE周长的最小值.
考点:轴对称-最短路线问题,正方形的性质
专题:
分析:由正方形性质的得出B、D关于AC对称,根据两点之间线段最短可知,连接DE,交AC于P,连接BP,则此时PB+PE的值最小,进而利用勾股定理求出即可.
解答: 解:(1)连接DE,交AC于P,连接BP,则此时PB+PE的值最小,即△BPE的周长最小;
解:(1)连接DE,交AC于P,连接BP,则此时PB+PE的值最小,即△BPE的周长最小;
(2)∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AB=8,
∴DE=
=10,
∴PB+PE的最小值是10,
∴△BPE周长的最小值=PB+PE+BE=10+2=12.
 解:(1)连接DE,交AC于P,连接BP,则此时PB+PE的值最小,即△BPE的周长最小;
解:(1)连接DE,交AC于P,连接BP,则此时PB+PE的值最小,即△BPE的周长最小;(2)∵四边形ABCD是正方形,
∴B、D关于AC对称,
∴PB=PD,
∴PB+PE=PD+PE=DE.
∵BE=2,AE=3BE,
∴AE=6,AB=8,
∴DE=
| 62+82 |
∴PB+PE的最小值是10,
∴△BPE周长的最小值=PB+PE+BE=10+2=12.
点评:本题考查了轴对称-最短路线问题,正方形的性质,解此题通常是利用两点之间,线段最短的性质得出.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果单项式
x3ya与
xby4是同类项,那么(-a)b的值是( )
| 2 |
| a |
| 3 |
| 4 |
| A、64 | B、-64 |
| C、81 | D、-81 |
单项式-0.6ab2的系数是( )
| A、-1 | B、0.6 |
| C、-6 | D、-0.6 |


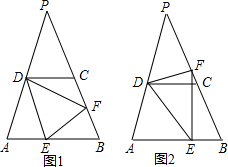 如图,在等腰△ABP中,PA=PB,点D、E分别为AP、AB边上的点,点C、F都在BP边长,且DC∥AB,DA=DC,∠EDF=
如图,在等腰△ABP中,PA=PB,点D、E分别为AP、AB边上的点,点C、F都在BP边长,且DC∥AB,DA=DC,∠EDF=