题目内容
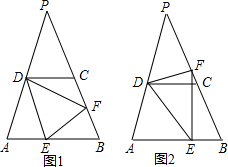 如图,在等腰△ABP中,PA=PB,点D、E分别为AP、AB边上的点,点C、F都在BP边长,且DC∥AB,DA=DC,∠EDF=
如图,在等腰△ABP中,PA=PB,点D、E分别为AP、AB边上的点,点C、F都在BP边长,且DC∥AB,DA=DC,∠EDF=| 1 |
| 2 |
(1)若F在BC边上时,求证:AE+CF=EF;
(2)若F在BC延长线上时,请写出AE、CF、EF的数量关系,并给出证明;
(3)若F在BC边上时,且AD=DC=1,AB=2,则△BEF的最大面积为
考点:全等三角形的判定与性质
专题:
分析:(1)延长EA至G,使AG=CF,连接GD,由条件可以证明△AGD≌△CFD,就有GD=FD,∠ADG=∠CDF,进而证明就可以得出结论;
(2)在EA上取一点M使AM=CF,由条件可以得出△ADM≌△CDF,就可以得出DM=DF,再证明△EDF≌△MDE就可以得出EF=ME,进而就可以得出结论;
(3)由条件AD=DC=1,AB=2及DC∥AB就可以得出△PAB为等边三角形,就有∠B=60°,作FH⊥AB于H,当设BF=x,AE=y,由三角形的面积公式就可以求出结论.
(2)在EA上取一点M使AM=CF,由条件可以得出△ADM≌△CDF,就可以得出DM=DF,再证明△EDF≌△MDE就可以得出EF=ME,进而就可以得出结论;
(3)由条件AD=DC=1,AB=2及DC∥AB就可以得出△PAB为等边三角形,就有∠B=60°,作FH⊥AB于H,当设BF=x,AE=y,由三角形的面积公式就可以求出结论.
解答:(1)证明:如图,
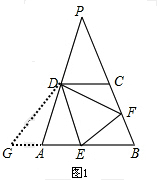
延长EA至G,使AG=CF,连接GD,
∵PA=PB,DC∥AB,
∴∠PAB=∠PBA,∠PCD=∠PBA,
∴∠PAB=∠PCD,
∴∠DAG=∠DCF,
又∵DA=DC,
∴△AGD≌△CFD.
∴GD=FD,∠ADG=∠CDF,
∵∠EDF=
∠ADC,
∴∠GDE=∠ADG+∠ADE=∠CDF+∠ADE=
∠ADC,
∴∠EDF=∠GDE,DE=DE,
∴△GDE≌△FDE.
∴EF=GE=AG+AE=CF+AE.
(2)EF=AE-CF.
如图
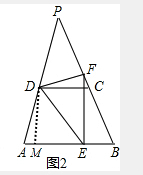
在AE上取一点M使AM=CF,
∵PA=PB,DC∥AB,
∴∠PAB=∠PBA,∠PCD=∠PBA,
∴∠PAB=∠PCD,
又∵DA=DC,
∴△ADM≌△CDF,
∴DM=DE,∠ADM=∠CDF,
∵∠EDF=
∠ADC,
∴∠MDE=∠MDF-∠EDF=∠MDC+∠CDF-∠EDF=∠MDC+∠ADM-∠EDF=∠ADC-
∠ADC=
∠ADC,
∴∠MDE=∠EDF,
又DE=DE,
∴△EDF≌△MDE
∴EF=ME=AE-AM=AE-CF.
(3)如图,
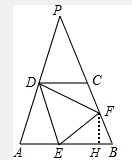
∵AD=DC=1,AB=2,DC∥AB,
DC为△PAB的中位线,
∴△PAB为等边三角形,
∴∠B=60°,
作FH⊥AB于H,设BF=x,AE=y,
S△BEF=
(2-y)×
x,
当x=1时,y=1,S△BEF最大为
.

延长EA至G,使AG=CF,连接GD,
∵PA=PB,DC∥AB,
∴∠PAB=∠PBA,∠PCD=∠PBA,
∴∠PAB=∠PCD,
∴∠DAG=∠DCF,
又∵DA=DC,
∴△AGD≌△CFD.
∴GD=FD,∠ADG=∠CDF,
∵∠EDF=
| 1 |
| 2 |
∴∠GDE=∠ADG+∠ADE=∠CDF+∠ADE=
| 1 |
| 2 |
∴∠EDF=∠GDE,DE=DE,
∴△GDE≌△FDE.
∴EF=GE=AG+AE=CF+AE.
(2)EF=AE-CF.
如图

在AE上取一点M使AM=CF,
∵PA=PB,DC∥AB,
∴∠PAB=∠PBA,∠PCD=∠PBA,
∴∠PAB=∠PCD,
又∵DA=DC,
∴△ADM≌△CDF,
∴DM=DE,∠ADM=∠CDF,
∵∠EDF=
| 1 |
| 2 |
∴∠MDE=∠MDF-∠EDF=∠MDC+∠CDF-∠EDF=∠MDC+∠ADM-∠EDF=∠ADC-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MDE=∠EDF,
又DE=DE,
∴△EDF≌△MDE
∴EF=ME=AE-AM=AE-CF.
(3)如图,

∵AD=DC=1,AB=2,DC∥AB,
DC为△PAB的中位线,
∴△PAB为等边三角形,
∴∠B=60°,
作FH⊥AB于H,设BF=x,AE=y,
S△BEF=
| 1 |
| 2 |
| ||
| 2 |
当x=1时,y=1,S△BEF最大为
| ||
| 4 |
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的对应角相等,对应边相等.

练习册系列答案
相关题目
已知x为任意实数,则多项式x-1-
x2的值( )
| 1 |
| 4 |
| A、一定为负数 |
| B、不可能为正数 |
| C、一定为正数 |
| D、为一切有理数 |
下列五个实数:
,(3-π)0,(-2)2,
-
,-|-3|,其中正数的和为( )
| 3 | -8 |
| 16 |
| 3 | 27 |
| A、4 | B、5 | C、6 | D、7 |
 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.
如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点.



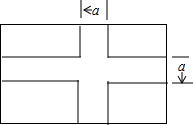 如图,是一个长方形草坪,长50m,宽30m.若在草坪中修两条长方形的小路,小路的宽均为am.
如图,是一个长方形草坪,长50m,宽30m.若在草坪中修两条长方形的小路,小路的宽均为am. 如图,直线y=-
如图,直线y=-