题目内容
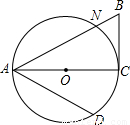
 已知:如图,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,连结PB、PO,PO∥BC,
已知:如图,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,连结PB、PO,PO∥BC,
(1)求证:直线PB是⊙O的切线;
(2)求tan∠BCA的值.
(1)证明:连接OB,
∵OB=OC,
∴∠C=∠OBC.
∵PO∥BC,
∴∠C=∠AOP,∠BOP=∠OBC,
∴∠AOP=∠BOP
∵OP=OP,
∴△AOP≌△BOP.
∴∠OBP=∠OAP=90°
∴PB是⊙O的切线.
(2)解:延长AC交PB的延长线于点D,
∵PO∥BC,
∴△PDO∽△BDC.

∴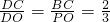 .
.
∴DC=2CO.
设CO=r,则DO=3r,连结BO,
在Rt△BDO中,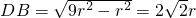 .
.
又∵△BDO∽△ADP,
∴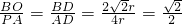 .
.
∴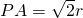 .
.
∴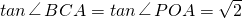 .
.
分析:(1)连接OB.证OB⊥PB即可.通过证明△AOP≌△BOP得证.
(2)延长AC交PB的延长线于点D,利用△PDO∽△BDC得到DC=2CO.设CO=r,则DO=3r,连结BO,利用△BDO∽△ADP,求得PA的长,从而求解结论.
点评:本题考查了全等三角形的判定与性质、相似三角形的判定与性质及切线的判定,特别是第(2)题,难度较大.
∵OB=OC,
∴∠C=∠OBC.
∵PO∥BC,
∴∠C=∠AOP,∠BOP=∠OBC,
∴∠AOP=∠BOP
∵OP=OP,
∴△AOP≌△BOP.
∴∠OBP=∠OAP=90°
∴PB是⊙O的切线.
(2)解:延长AC交PB的延长线于点D,
∵PO∥BC,
∴△PDO∽△BDC.

∴
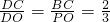 .
.∴DC=2CO.
设CO=r,则DO=3r,连结BO,
在Rt△BDO中,
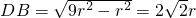 .
.又∵△BDO∽△ADP,
∴
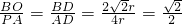 .
.∴
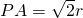 .
.∴
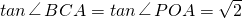 .
.分析:(1)连接OB.证OB⊥PB即可.通过证明△AOP≌△BOP得证.
(2)延长AC交PB的延长线于点D,利用△PDO∽△BDC得到DC=2CO.设CO=r,则DO=3r,连结BO,利用△BDO∽△ADP,求得PA的长,从而求解结论.
点评:本题考查了全等三角形的判定与性质、相似三角形的判定与性质及切线的判定,特别是第(2)题,难度较大.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 3、已知:如图,AC为正方形ABCD的对角线,E为AC上一点,连接EB,ED,当∠BED=126°时,∠EDA的度数为( )
3、已知:如图,AC为正方形ABCD的对角线,E为AC上一点,连接EB,ED,当∠BED=126°时,∠EDA的度数为( ) (1997•贵阳)已知:如图,AC为⊙O的直径,BC为⊙O的切线,C为切点,且劣弧CN=弧CD,求证:
(1997•贵阳)已知:如图,AC为⊙O的直径,BC为⊙O的切线,C为切点,且劣弧CN=弧CD,求证: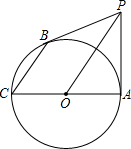 (2013•大兴区一模)已知:如图,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,连结PB、PO,PO∥BC,
(2013•大兴区一模)已知:如图,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,连结PB、PO,PO∥BC,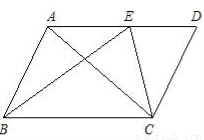
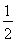
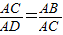 .
.