Question

已知，如图，AC为平行四边形ABCD的对角线，点E是边AD上一点，

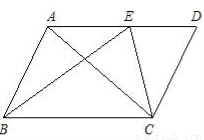
（1）若∠CAD=∠EBC，AC=BE，AB=6，求CE的长。

（2）若AE+AB=BC,求证：∠BEC=∠ABE+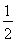∠BAD.

 

Answer 1

【答案】

（1）6；（2）证明见解析.

【解析】

试题分析：（1）由四边形ABCD是平行四边形知∠CAD=∠BCA，从而∠BCA=∠EBC，易证△BCA≌△CBE，因此CE=AB=6；

（2）过A作AA′∥CE交BC于A′，交BE于点F，可知四边形AA′CE为平行四边形，所以AE=A′C，∠CEB=∠EFA，∠AA′B=∠EAA′;又AE+AB=BC，∠BAA′=∠B A′A，易证∠BEC=∠ABE+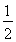∠BAD.

试题解析：∵四边形ABCD是平行四边形，

∴AD∥BC

∴∠CAD=∠BCA，

∴∠BCA=∠EBC

又：AC=BE，BC=CB

∴△BCA≌△CBE

∴CE=AB=6.

（２）过A作AA′∥CE交BC于A′，交BE于点F，

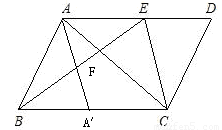
∴四边形AA′CE是平行四边形

∴∠CEB=∠EFA，∠AA′B=∠E AA′，AE= A′C

又：AE+AB=BC，

∴AB=BA′

∴∠BAA′=∠B A′A=∠E AA′=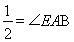

又：∠EFA=∠ABE+∠BAF

∴∠BEC=∠ABE+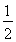∠BAD.

考点: 1.平行四边形的判定与性质；2.全等三角形的判定与性质；3.等腰三角形的性质.