题目内容
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,连接
,连接![]() ,将
,将![]() 绕
绕![]() 点作顺时针方向旋转得到
点作顺时针方向旋转得到![]() (
(![]() 与
与![]() 重合),且点
重合),且点![]() 刚好落在
刚好落在![]() 的延长上,
的延长上,![]() 与
与![]() 相交于点
相交于点![]() .
.
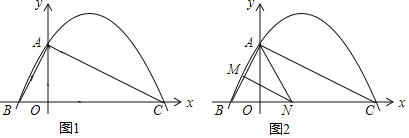
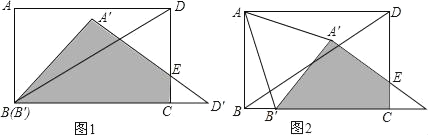
(1)求矩形![]() 与
与![]() 重叠部分(如图1中阴影部分
重叠部分(如图1中阴影部分![]() )的面积;
)的面积;
(2)将![]() 以每秒2
以每秒2![]() 的速度沿直线
的速度沿直线![]() 向右平移,如图2,当
向右平移,如图2,当![]() 移动到
移动到![]() 点时停止移动.设矩形
点时停止移动.设矩形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() ,移动的时间为
,移动的时间为![]() ,请你直接写出
,请你直接写出![]() 关于
关于![]() 的函数关系式,并指出自变量
的函数关系式,并指出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的平移过程中,是否存在这样的时间![]() ,使得
,使得![]() 成为等腰三角形?若存在,请你直接写出对应的
成为等腰三角形?若存在,请你直接写出对应的![]() 的值,若不存在,请你说明理由.
的值,若不存在,请你说明理由.
【答案】(1)![]() ;(2)
;(2)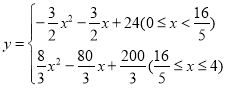 ;(3)存在,使得
;(3)存在,使得![]() 成为等腰三角形的
成为等腰三角形的![]() 的值有:0秒、
的值有:0秒、![]() 秒、
秒、![]() .
.
【解析】
(1)先用勾股定理求出BD的长,再根据旋转的性质得出![]() ,
,![]() ,利用
,利用![]() 的正切值求出
的正切值求出![]() 的值,利用三角形的面积差即可求阴影部分的面积;
的值,利用三角形的面积差即可求阴影部分的面积;
(2)分类讨论,当![]() 时和当
时和当![]() 时,分别列出函数表达式;
时,分别列出函数表达式;
(3)分类讨论,当![]() 时;当
时;当![]() 时;当
时;当![]() 时,根据勾股定理列方程即可.
时,根据勾股定理列方程即可.
解:(1)![]() ,
,![]() ,
,
![]() ,
,
根据旋转的性质可知![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)①当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
②当![]() 时,
时,![]() ,
,![]()
![]() .
.
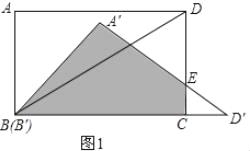
(3)①如图1,当![]() 时,
时,![]() 秒;
秒;
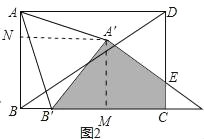
②如图2,当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() 秒,(
秒,(![]() 舍去);
舍去);
③如图2,当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]()
解得:![]() 秒.
秒.
综上所述:使得![]() 成为等腰三角形的
成为等腰三角形的![]() 的值有:0秒、
的值有:0秒、![]() 秒、
秒、![]() .
.

练习册系列答案
相关题目