题目内容
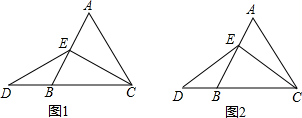
10.在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且AE=BD.试探索以下问题:(1)当点E为AB的中点时,如图1,求证:EC=ED.
(2)如图2,当点E不是AB的中点时,过点E作EF∥BC,交AC于点F,求证:△AEF是等边三角形.
(3)在(2)的条件下,EC与ED还相等吗?请说明理由.
分析 (1)根据等边三角形的性质得出AB=AC=BC,∠ABC=∠ACB=∠A=60°,再由E是AB的中点,AE=BE=BD,证出∠EDB=∠ECB,得出EC=ED;
(2)在△AEF中,只要证明有两个内角是60°即可;
(3)只要证明△DBE≌△EFC,即可推出结论;
解答 证明:(1)∵△ABC是等边三角形,
∴AB=AC=BC,∠ABC=∠ACB=∠A=60°,
∵E是AB的中点,
∴AE=BE,∠ECB=$\frac{1}{2}$∠ACB=30°,
∵AE=BD,
∴BE=BD,
∴∠EDB=∠DEB=$\frac{1}{2}$∠ABC=30°,
∴∠EDB=∠ECB,
∴EC=ED.
(2)过E点作EF∥BC交AC于F点.如图2所示: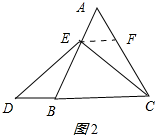
∵EF∥BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°,
∴△AEF是等边三角形.
(3)ED=EC. 理由如下:
∵△AEF是等边三角形.
∴∠AFE=∠ABC=60°
∴∠EFC=∠DBE=120°,
又∵AE=BD,AB=AC,
∴BD=EF,BE=FC,
在△DBE和△EFC中,
$\left\{\begin{array}{l}{BD=EF}\\{∠DBE=∠EFC}\\{BE=FC}\end{array}\right.$,
∴△DBE≌△EFC(SAS),
∴ED=EC.
点评 本题考查了等边三角形的性质和判定、全等三角形的判定与性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 观察图形由(1)→(2)的变化过程,写出A、B对应点的坐标分别为(2,-3),(4,-1).
观察图形由(1)→(2)的变化过程,写出A、B对应点的坐标分别为(2,-3),(4,-1).