题目内容
有若干个数,第一个数记作a1,第二个数记作a2,第三个数记作a3…,第n个数记作an,若a1=-0.5,从第二个数开始,每个数都等于1与它前面的数差的倒数.
(1)计算
a2=______;
a3=______;
a4=______.
(2)猜想
a1998=______;
a2000=______.
解:由题意得:a2= =
= ,
,
a3= =3,
=3,
a4= =-
=- ,
,
不难发现 ,
, ,3这三个数反复出现.
,3这三个数反复出现.
∵1998÷3=666,其余数为0,
∴a1998=a3=3;
∵2000÷3的余数是2,所以a2000=a2= .
.
故答案为: ,3,-
,3,- ;3,
;3, .
.
分析:根据规定进行计算,发现:a1= ,a2=
,a2= ,a3=3,a4=-
,a3=3,a4=- .从而发现3个一循环.按照这个规律计算即可.
.从而发现3个一循环.按照这个规律计算即可.
点评:本题考查规律型中的数字变化问题,难度适中,关键是正确计算发现循环的规律,然后进行分析判断.
 =
= ,
,a3=
 =3,
=3,a4=
 =-
=- ,
,不难发现
 ,
, ,3这三个数反复出现.
,3这三个数反复出现.∵1998÷3=666,其余数为0,
∴a1998=a3=3;
∵2000÷3的余数是2,所以a2000=a2=
 .
.故答案为:
 ,3,-
,3,- ;3,
;3, .
.分析:根据规定进行计算,发现:a1=
 ,a2=
,a2= ,a3=3,a4=-
,a3=3,a4=- .从而发现3个一循环.按照这个规律计算即可.
.从而发现3个一循环.按照这个规律计算即可.点评:本题考查规律型中的数字变化问题,难度适中,关键是正确计算发现循环的规律,然后进行分析判断.

练习册系列答案
相关题目
 ,从第二个数起,每个数都等于“1”与它前面的那个数的差的倒数.
,从第二个数起,每个数都等于“1”与它前面的那个数的差的倒数.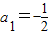 ,从第二个数起,每个数都等于“1”与它前面的那个数的差的倒数.
,从第二个数起,每个数都等于“1”与它前面的那个数的差的倒数.