题目内容
20.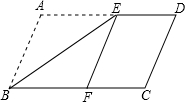 如图,四边形ABCD是平行四边形,AD>AB,∠ABC的平分线BE交AD于点E,将△ABE沿直线BE折叠,使得点A落在BC边的点F上,请判断四边形ABFE的形状,并说明理由.
如图,四边形ABCD是平行四边形,AD>AB,∠ABC的平分线BE交AD于点E,将△ABE沿直线BE折叠,使得点A落在BC边的点F上,请判断四边形ABFE的形状,并说明理由.
分析 根据平行四边形的性质以及翻折变换的性质得出∠ABE=∠AEB,AB=BF,即可得出AB=AE=BF,于是得到结论.
解答 解:四边形ABFE是菱形
理由:∵E为?ABCD中AD边上的一点,
∴AD∥BC,
∴∠AEB=∠EBF,
∵将△ABE沿BE折叠使得点A刚好落在BC边上的F点处,
∴∠ABE=∠EBF,AB=BF,
∴∠ABE=∠AEB,
∴AB=AE,
∴AE=BF,
∵AE∥BF,
∴四边形ABFE是菱形.
点评 此题主要考查了翻折变换的性质以及平行四边形的性质,根据已知得出∠ABE=∠AEB是解题关键.

练习册系列答案
相关题目
14.$\sqrt{5}$的相反数是( )
| A. | $\sqrt{5}$ | B. | -$\sqrt{5}$ | C. | -$\frac{1}{{\sqrt{5}}}$ | D. | $\frac{1}{{\sqrt{5}}}$ |
15.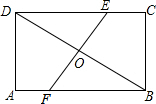 如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
 如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )
如图,在矩形ABCD中,AB=8,BC=6,EF是BD的中垂线,则EF=( )| A. | $\frac{15}{4}$ | B. | 5 | C. | 8 | D. | $\frac{15}{2}$ |
 一个正方体的平面展开图如图,已知正方体相对两个面上的数之和相等,则a=-3,b=2.
一个正方体的平面展开图如图,已知正方体相对两个面上的数之和相等,则a=-3,b=2.
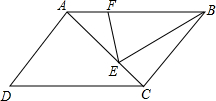 平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积.
平行四边形ABCD中,E在AC上,AE=2EC,F在AB上,BF=2AF,如果△BEF的面积为2cm2,求平行四边形ABCD的面积.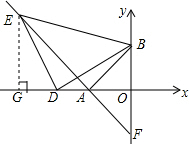 在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6).
在平面直角坐标系xOy中,直线AB与x轴交于点A(-6,0),与y轴交于点B(0,6). 如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°.
如图,直线AB⊥l1,l1∥l2,∠1=75°,则∠2的大小为165°.