题目内容
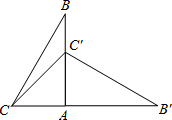 如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为________度.
如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为________度.
105
分析:利用旋转中心为点A,C、C′为对应点,可知AC=AC′,又∠CAC′=90°,根据△CAC′的特性得出,∠CC′A=45°以及∠AC′B′=60°即可得出答案.
解答:由旋转的性质可知,AC=AC′,∠ACB=∠AC′B′=60°,
又因为∠CAC′=90°,可知△CAC′为等腰直角三角形,
所以,∠CC′A=45°,
∵∠ACB=∠AC′B′=60°,
∴∠CC′B′的度数为:∠CC′A+∠AC′B′=45°+60°=105°.
故答案为:105.
点评:此题主要考查了旋转的性质,利用对应点与旋转中心的连线相等,夹角是旋转角进而得出是解题关键.
分析:利用旋转中心为点A,C、C′为对应点,可知AC=AC′,又∠CAC′=90°,根据△CAC′的特性得出,∠CC′A=45°以及∠AC′B′=60°即可得出答案.
解答:由旋转的性质可知,AC=AC′,∠ACB=∠AC′B′=60°,
又因为∠CAC′=90°,可知△CAC′为等腰直角三角形,
所以,∠CC′A=45°,
∵∠ACB=∠AC′B′=60°,
∴∠CC′B′的度数为:∠CC′A+∠AC′B′=45°+60°=105°.
故答案为:105.
点评:此题主要考查了旋转的性质,利用对应点与旋转中心的连线相等,夹角是旋转角进而得出是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
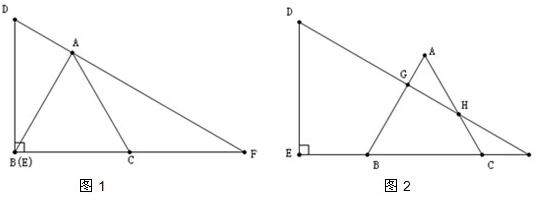
 如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为
如图,将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′,则∠CC′B′的度数为