题目内容
如图，将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′，则∠CC′B′的度数为______度．
由旋转的性质可知，AC=AC′，∠ACB=∠AC′B′=60°，
又因为∠CAC′=90°，可知△CAC′为等腰直角三角形，
所以，∠CC′A=45°，
∵∠ACB=∠AC′B′=60°，
∴∠CC′B′的度数为：∠CC′A+∠AC′B′=45°+60°=105°．
故答案为：105．
又因为∠CAC′=90°，可知△CAC′为等腰直角三角形，
所以，∠CC′A=45°，
∵∠ACB=∠AC′B′=60°，
∴∠CC′B′的度数为：∠CC′A+∠AC′B′=45°+60°=105°．
故答案为：105．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图，将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′，则∠CC′B′的度数为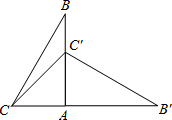
如图，将一块含有30°角的三角板△ABC绕着点A顺时针旋转90°后得到△AB′C′，则∠CC′B′的度数为________度．