题目内容
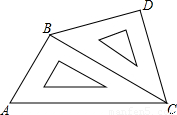
 将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
将两个三角板的两个直角的顶点O重合在一起,放置成如图所示的位置.
(1)如果重叠在一起∠BOC=40°,猜想∠AOD=______;
(2)如果重叠在一起∠BOC=50°,猜想∠AOD=______;
(3)在(1)、(2)中,计算∠AOD+∠BOC=______;
(4)由此可知,三角板AOB绕重合点O旋转,不论旋转到任何位置,∠AOD与∠BOC始终满足______的关系;
(5)图中∠AOC与∠BOD满足______的关系,根据是______.
解:(1)由∠AOD=∠AOB+∠COD-∠BOC,
当∠BOC=40°,
∴∠AOD=140°,
(2)由(1)知,∠AOD=130°,
(3)猜想∠AOD+∠BOC=180°,
(4)设∠BOC=α,
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,
故∠AOD+∠BOC=180°,即∠AOD与∠BOC始终满足互补的关系;
(5)图中∠AOC与∠BOD满足 相等的关系,根据是 同角的余角相等.
故答案为:140°,130°,180°,互补;相等,同角的余角相等.
分析:(1)、(2)均利用∠AOD=∠AOB+∠COD-∠BOC得到∠AOD,故(3)可猜想∠AOD+∠BOC=180°;
(4)设∠BOC=α,∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,故可得到结论;
(5)根据余角的性质得到∠AOC与∠BOD满足的关系.
点评:本题主要考查角的比较与运算,充分利用∠AOD=∠AOB+∠COD-∠BOC解答此题.
当∠BOC=40°,
∴∠AOD=140°,
(2)由(1)知,∠AOD=130°,
(3)猜想∠AOD+∠BOC=180°,
(4)设∠BOC=α,
∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,
故∠AOD+∠BOC=180°,即∠AOD与∠BOC始终满足互补的关系;
(5)图中∠AOC与∠BOD满足 相等的关系,根据是 同角的余角相等.
故答案为:140°,130°,180°,互补;相等,同角的余角相等.
分析:(1)、(2)均利用∠AOD=∠AOB+∠COD-∠BOC得到∠AOD,故(3)可猜想∠AOD+∠BOC=180°;
(4)设∠BOC=α,∠AOD+∠BOC=∠AOB+∠BOD+∠BOC=∠AOB+∠COD=180°,故可得到结论;
(5)根据余角的性质得到∠AOC与∠BOD满足的关系.
点评:本题主要考查角的比较与运算,充分利用∠AOD=∠AOB+∠COD-∠BOC解答此题.

练习册系列答案
相关题目
 如图,O是AB上一点,∠DOA=90°,∠AOC=∠BOE,则图中两个角的和为直角的角共有
如图,O是AB上一点,∠DOA=90°,∠AOC=∠BOE,则图中两个角的和为直角的角共有 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)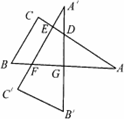
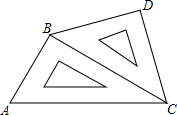 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)