题目内容
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)若已知CD=2,求AC的长.
请你先阅读并完成解法一,然后利用锐角三角函数的知识写出与解法一不同的解法.
解法一:在Rt△ABC中,∵BD=CD=2
∴由勾股定理,BC=
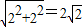
在Rt△ABC中,设AB=x
∵∠BCA=30°,∴AC=2AB=2x
由勾股定理,AB2+BC2=AC2,即
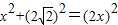
∵x>0,解得x=______
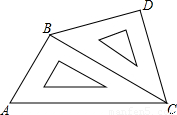
【答案】分析:先根据方程求出AB的值,再求出AC的值,第二种方法在直角△BDC中根据勾股定理得到BC的长,进而在直角△ABC中,根据勾股定理,求出AC的长.
解答:解:∵BD=CD=2,
∴在Rt△ADC中, ,
,
∴设AB=x,则AC=2x,
∴ ,
,
∴x2+8=4x2,
∴3x2=8,
∴x2= ,
,
∴x= ,
,
AC=2AB= .
.
故答案为: ,
, .
.
第二种方法:在Rt△BCD中,CD=2,∠DBC=45°,
∴BC= =
= =2
=2
在Rt△BAC中,∠BCA=30°,
∴AC= =
= =
= .
.
点评:本题主要考查根据特殊角的三角函数值解直角三角形与勾股定理的运用,本题解决的关键是利用勾股定理,先求出两个直角三角形的公共边BC.
解答:解:∵BD=CD=2,
∴在Rt△ADC中,
 ,
,∴设AB=x,则AC=2x,
∴
 ,
,∴x2+8=4x2,
∴3x2=8,
∴x2=
 ,
,∴x=
 ,
,AC=2AB=
 .
.故答案为:
 ,
, .
.第二种方法:在Rt△BCD中,CD=2,∠DBC=45°,
∴BC=
 =
= =2
=2
在Rt△BAC中,∠BCA=30°,
∴AC=
 =
= =
= .
.点评:本题主要考查根据特殊角的三角函数值解直角三角形与勾股定理的运用,本题解决的关键是利用勾股定理,先求出两个直角三角形的公共边BC.

练习册系列答案
相关题目
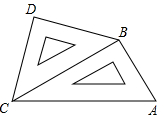 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知CD=2,求AC的长.
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知CD=2,求AC的长. 小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长.(两个三角板分别是等腰直角三角形和含30°的直角三角形)
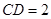 ,求
,求 的长?
的长?
 ,求
,求 的长?
的长?