题目内容
为了了解某次运动会2000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题而言,下列说法正确的是( )
| A、2000名运动员是主体 |
| B、每名运动员是个体 |
| C、100名运动员是抽取的一个样本 |
| D、这种调查方式是抽样调查 |
考点:总体、个体、样本、样本容量
专题:
分析:总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答:解:A、2000名运动员的年龄是主体,故A错误;
B、每名运动员的年龄是个体,故B错误;
C、从中抽查了100名运动员的年龄是一个样本,故C错误;
D、这种方式是抽样调查,故D正确;
故选:D.
B、每名运动员的年龄是个体,故B错误;
C、从中抽查了100名运动员的年龄是一个样本,故C错误;
D、这种方式是抽样调查,故D正确;
故选:D.
点评:本题考查了总体、个体、样本、样本容量,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位

练习册系列答案
相关题目
使分式
有意义,x的取值范围是( )
| x+2 |
| x+3 |
| A、x≠3 | B、x≠-3 |
| C、x>-2 | D、x<2 |
已知坐标原点既是抛物线y=(3a-2)x2的最低点,又是抛物线y=(a-2)x2的最高点,若a为整数,则函数y=(a-2)xa+1+ax+a-3是( )
| A、二次函数 | B、一次函数 |
| C、反比例函数 | D、正比例函数 |
某电视台每播放18分钟节目便插播2分钟广告,打开电视收看该台恰好遇到广告的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
 已知:如图,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,CF平分∠BCD.
已知:如图,四边形ABCD中,∠B=∠D=90°,AE平分∠DAB,CF平分∠BCD.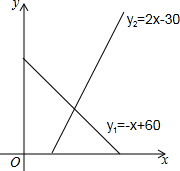 某地区一种商品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-30.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量.
某地区一种商品的需求量y1(万件),供应量y2(万件)与价格x(元/件)分别近似满足下列函数关系式:y1=-x+60,y2=2x-30.需求量为0时,即停止供应.当y1=y2时,该商品的价格称为稳定价格,需求量称为稳定需求量.