题目内容
12.顺次连接矩形的四边中点所得的四边形一定是( )| A. | 菱形 | B. | 矩形 | C. | 平行四边形 | D. | 正方形 |
分析 因为题中给出的条件是中点,所以可利用三角形中位线性质,以及矩形对角线相等去证明四条边都相等,从而说明是一个菱形.
解答 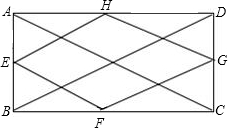 解:连接AC、BD,
解:连接AC、BD,
在△ABD中,
∵AH=HD,AE=EB
∴EH=$\frac{1}{2}$BD,
同理FG=$\frac{1}{2}$BD,HG=$\frac{1}{2}$AC,EF=$\frac{1}{2}$AC,
又∵在矩形ABCD中,AC=BD,
∴EH=HG=GF=FE,
∴四边形EFGH为菱形.
故选A.
点评 本题考查了菱形的判定,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义,②四边相等,③对角线互相垂直平分.

练习册系列答案
相关题目
1.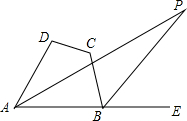 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=200°,则∠P=( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
17.函数y=-2(x-1)2+3的图象的顶点坐标是( )
| A. | (1,-4) | B. | (-1,2) | C. | (-1,3) | D. | (1,3) |
1.下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择甲.
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 185 | 180 | 185 | 180 |
| 方差 | 3.6 | 3.6 | 7.4 | 8.1 |
2.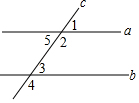 如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
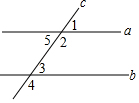 如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )
如图,直线a,b被直线c所截,∠1=55°,下列条件能推出a∥b的是( )| A. | ∠3=55° | B. | ∠2=55° | C. | ∠4=55° | D. | ∠5=55° |
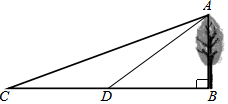 如图,为了测树AB的高,李明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助李明计算出树的高度为10米.
如图,为了测树AB的高,李明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助李明计算出树的高度为10米.