题目内容
3.已知x-$\frac{1}{x}$=3,求x2+$\frac{1}{{x}^{2}}$和x4+$\frac{1}{{x}^{4}}$的值.分析 把该式子两边平方后可以求得x2+$\frac{1}{{x}^{2}}$的值,再次平方即可得到x4+$\frac{1}{{x}^{4}}$的值.
解答 解:∵x-$\frac{1}{x}$=3,(x-$\frac{1}{x}$)2=x2+$\frac{1}{{x}^{2}}$-2
∴x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2=32+2=11.
x4+$\frac{1}{{x}^{4}}$=(x2+$\frac{1}{{x}^{2}}$)2-2=112-2=119.
点评 本题考查了完全平方公式,利用x和$\frac{1}{x}$互为倒数乘积是1与完全平方公式来进行解题.

练习册系列答案
相关题目
3.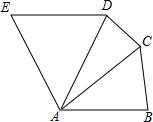 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
 如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )| A. | 150° | B. | 160° | C. | 130° | D. | 60° |
11.如果a是负数,那么9a2的平方根是( )
| A. | 3a | B. | -3a | C. | ±3a | D. | ±3$\sqrt{a}$ |
13.计算:211-210的结果是( )
| A. | -210 | B. | 2 | C. | -2 | D. | 210 |
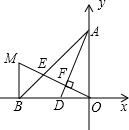 如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.
如图,A(0,4),B(-4,0),D(-2,0),OE⊥AD于F,交AB于E,BM⊥OB交OE的延长线于M.