题目内容
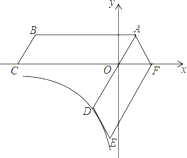
【题目】如图,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,且AO:OD=1:2,点F恰好落在x轴的正半轴上,若点C(﹣6,0),点D在反比例函数y=![]() 的图象上.
的图象上.
(1)证明:△AOF是等边三角形,并求k的值;
(2)在x轴上有一点G,且△ACG是等腰三角形,求点G的坐标;
(3)求旋转过程中四边形ABCO扫过的面积;
【答案】(1)证明见解析; k=![]() ; (2) ( 8, 0) ,(
; (2) ( 8, 0) ,(![]() ,0 ) (
,0 ) (![]() ),(
),(![]() ,0) ;(3) S=
,0) ;(3) S=![]() .
.
【解析】试题分析:(1)由旋转的性质可知AO=AF,且∠AOF=∠BAO=∠OAF,可证得△AOF为等边三角形,由题意可求得OA、OD的长,过D作DK⊥x轴于点K,则可求得OK和DK的长,可求得D点坐标,代入反比例函数解析式可求得k的值;
(2)设G(x,0),由A、C的坐标可分别表示出AG、CG和AC的长,分AG=CG、AG=AC和CG=AC三种情况分别得到关于x的方程,可求得x的值,则可求得G点坐标;
(3)过A作AH⊥x轴于H.可求得AH的长.由旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积,即可得出结论.
试题解析:解:(1)过D作DK⊥x轴于K.由旋转的性质可得AO=AF=DE=BC,∠BAO=∠OAF.∵AB∥BC,∴∠BAO=∠AOF,∴∠AOF=∠OAF,∴AF=OF,∴AF=OF=OA,∴△AOF为等边三角形.设D(x,y).∵C(﹣6,0),∴OC=6,∴AD=CO=6.∵AO:OD=1:2,∴AO=2,OD=4.∵∠COD=∠AOF=60°,∴OK=![]() OD=2,DK=
OD=2,DK=![]() OK=
OK=![]() .∵x<0,y<0,∴x=-2,y=-
.∵x<0,y<0,∴x=-2,y=-![]() ,∴D(-2,-
,∴D(-2,- ![]() ),∴k=-2×(-
),∴k=-2×(-![]() )=
)=![]() .
.

(2)设G(x,0),且A(1, ![]() ),C(﹣6,0),∴AG=
),C(﹣6,0),∴AG=![]() =
=![]() ,CG=|x+6|,AC=
,CG=|x+6|,AC=![]() =
=![]() .∵△ACG是等腰三角形,∴有AG=CG、AG=AC和CG=AC三种情况:
.∵△ACG是等腰三角形,∴有AG=CG、AG=AC和CG=AC三种情况:
①当AG=CG时,则![]() =|x+6|,解得x=﹣
=|x+6|,解得x=﹣![]() ,此时G点坐标为(﹣
,此时G点坐标为(﹣![]() ,0);
,0);
②当AG=AC时,则![]() =
=![]() ,解得x=﹣6(与C点重合,舍去)或x=8,此时G点坐标为(8,0);
,解得x=﹣6(与C点重合,舍去)或x=8,此时G点坐标为(8,0);
③当CG=AC时,则|x+6|=![]() ,解得x=﹣6+
,解得x=﹣6+![]() 或x=﹣6﹣
或x=﹣6﹣![]() ,此时G点坐标为(﹣6+
,此时G点坐标为(﹣6+![]() ,0)或(﹣6﹣
,0)或(﹣6﹣![]() ,0);
,0);
综上可知G点坐标为(﹣![]() ,0)或(8,0)或(﹣6+
,0)或(8,0)或(﹣6+![]() ,0)或(﹣6﹣
,0)或(﹣6﹣![]() ,0);
,0);
(3)如图2,过A作AH⊥x轴于H.∵OA=2,∠AOH=60°,∴AH=AOsin60°=![]() =
=![]() .AC=
.AC=![]() ,旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积=
,旋转角=∠CAE=∠OAF=60°,四边形ABCO扫过的面积=扇形CAE的面积+平行四边形ABCO的面积=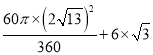 =
=![]() .
.


【题目】阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
电视机 | 电饭煲 | |
甲商店/元 | 100 | 60 |
乙商店/元 | 80 | 50 |
(1)设集团调配给甲商店x台电视机,则调配给甲商店电饭煲 台,调配给乙商店电视机 台、电饭煲 台;
(2)求出x的取值范围;
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.