题目内容
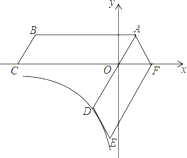
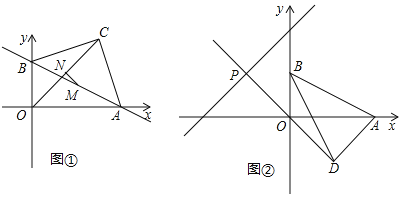
【题目】如图①，在平面直角坐标系中，直线y=12x+2与
交坐标轴于A,B两点．以AB为斜边在第一象限作等腰直角三角形ABC，C为直角顶点，连接OC．
（1）求线段AB的长度
（2）求直线BC的解析式；
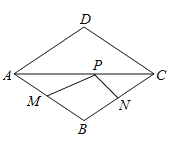
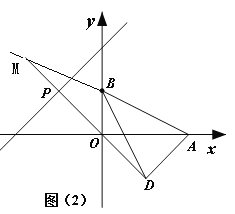
（3）如图②，将线段AB绕B点沿顺时针方向旋转至BD，且
，直线DO交直线y=x+3
于P点，求P点坐标．
【答案】（1）
；（2）
；（3）P点的坐标是
.
【解析】
（1）先确定出点A，B坐标，利用勾股定理计算即可；
（2）如图1中，作CE⊥x轴于E，作CF⊥y轴于F，进而判断出
，即可判断出四边形OECF是正方形，求出点C坐标即可解决问题．
（3）如图2中，先判断出点B是AM的中点，进而求出M的坐标，即可求出DP的解析式，联立
成方程组求解即可得出结论．
解：（1）∵直线
交坐标轴于A、B两点．
∴令
，
，∴B点的坐标是
，
，
令
，
，∴A点的坐标是
，
，
根据勾股定理得：
.
（2）如图，作CE⊥x轴于E，作CF⊥y轴于F，
∴四边形OECF是矩形．
∵
是等腰直角三角形，
，
，
，
，
，
，
．
∴四边形OECF是正方形，
，
，
，
．
∴C点坐标
设直线BC的解析式为：
，
∴将
、
代入得：
，
解得：
，
．
∴直线BC的解析式为：.
（3）延长AB交DP于M，
由旋转知，BD＝AB，
∴∠BAD＝∠BDA，
∵AD⊥DP，
∴∠ADP＝90°，
∴∠BDA＋∠BDM＝90°，∠BAD＋∠AMD＝90°，
∴∠AMD＝∠BDM，
∴BD＝BM，
∴BM＝AB，
∴点B是AM的中点，
∵A（4，0），B（0，2），
∴M（4，4），
∴直线DP的解析式为y＝x，
∵直线DO交直线y＝x＋3于P点，
将直线与
联立得：
解得：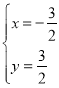
∴P点的坐标是.
练习册系列答案
习题精选系列答案
相关题目
