题目内容
如图所示，AD∥BC，∠B=90°，E是AB的中点，且DE平分∠ADC，求证：CE平分∠BCD．（提示：过点E作EF⊥CD于点F）考点：角平分线的性质
专题：证明题
分析：过点E作EF⊥CD，垂足为F，利用角平分线的性质以及其判定得出即可．
解答：证明：过点E作EF⊥CD，垂足为F．
∵AD∥BC，∠B=90°，
∴∠A=90°．
∵DE平分∠ADC，∠A=90°，EF⊥CD于F，
∴EA=EF．
∵E是AB的中点，
∴AE=BE，
∴EF=BE，
∵∠B=90°，EF⊥CD于F，
∴CE平分∠BCD．
证明：过点E作EF⊥CD，垂足为F．∵AD∥BC，∠B=90°，
∴∠A=90°．
∵DE平分∠ADC，∠A=90°，EF⊥CD于F，
∴EA=EF．
∵E是AB的中点，
∴AE=BE，
∴EF=BE，
∵∠B=90°，EF⊥CD于F，
∴CE平分∠BCD．
点评：本题考查的是角平分线的判定与性质，根据题意做出辅助线是解答此题的关键．用到的知识点：角平分线的性质：角平分线上的点到角的两边的距离相等．角平分线的判定：角的内部到角两边的距离相等的点在角的平分线上．
练习册系列答案
相关题目
如图，△ABC绕点下面几何体的截面图可能是圆的是（ ）
| A、正方体 | B、棱柱 |
| C、圆锥 | D、三棱锥 |
某商店把一件商品按进价增加20%作为定价，可是总卖不出去，后来老板把定价降低20%，以48元的价格出售，很快就卖出了，则老板卖出这件商品的盈亏情况是（ ）
| A、亏2元 | B、亏4元 |
| C、赚4元， | D、不亏不赚 |
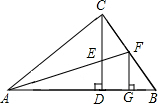如图，CD为Rt△ABC斜边上的高，∠BAC的平分线分别交CD、BC于点E、F．且FG⊥AB，垂足为G，把ab=
cd写成比例式，下列写法不正确的是（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|