题目内容
如图，BD是⊙O的直径，∠A=58°，则∠CBD的度数为________．
32°
分析：由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得∠D的度数，又由BD是⊙O的直径，根据直径所对的圆周角是直角，即可求得∠BCD=90°，继而求得∠CBD的度数．
解答：∵∠A与∠D是
对的圆周角，
∴∠D=∠A=58°，
∵BD是⊙O的直径，
∴∠ACD=90°，
∴∠CBD=90°-∠D=90°-58°=32°．
故答案为：32°．
点评：此题考查了圆周角定理与直角三角形的性质．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等与直径所对的圆周角等于直角定理的应用，注意数形结合思想的应用．
分析：由在同圆或等圆中，同弧或等弧所对的圆周角相等，即可求得∠D的度数，又由BD是⊙O的直径，根据直径所对的圆周角是直角，即可求得∠BCD=90°，继而求得∠CBD的度数．
解答：∵∠A与∠D是
对的圆周角，∴∠D=∠A=58°，
∵BD是⊙O的直径，
∴∠ACD=90°，
∴∠CBD=90°-∠D=90°-58°=32°．
故答案为：32°．
点评：此题考查了圆周角定理与直角三角形的性质．此题比较简单，注意掌握在同圆或等圆中，同弧或等弧所对的圆周角相等与直径所对的圆周角等于直角定理的应用，注意数形结合思想的应用．
练习册系列答案
相关题目
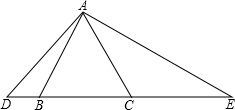如图，△ABC是一个边长为2的等边三角形，D、E都在直线BC上，并且∠DAE=120°
（2012•渝北区一模）如图，等边△ABC的边AB与正方形DEFG的边长均为2，且AB与DE在同一条直线上，开始时点B与点D重合，让△ABC沿这条直线向右平移，直到点B与点E重合为止，设BD的长为x，△ABC与正方形DEFG重叠部分（图中阴影部分）的面积为y，则y与x之间的函数关系的图象大致是（ ）
泰勒斯是古希腊哲学家，相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离．如图，B是观察点，船A在B的正前方，过B作AB的垂线，在垂线上截取任意长BD，C是BD的中点，观察者从点D沿垂直于BD的DE方向走，直到点E、船A和点C在一条直线上，那么△ABC≌△EDC，从而量出DE的距离即为船离岸的距离AB，这里判定△ABC≌△EDC的方法是（ ）
