题目内容
11.若a,b为有理数,且$\sqrt{18}$+$\sqrt{9}$$+\sqrt{\frac{1}{8}}$=a+b$\sqrt{2}$,求5a-4b的值.分析 将$\sqrt{18}$+$\sqrt{9}$$+\sqrt{\frac{1}{8}}$进行化简合项,即可得知a、b的值,将其代入5a-4b求出结果.
解答 解:∵$\sqrt{18}$+$\sqrt{9}$$+\sqrt{\frac{1}{8}}$=3$\sqrt{2}$+3+$\frac{1}{4}$$\sqrt{2}$=3+$\frac{13}{4}$$\sqrt{2}$=a+b$\sqrt{2}$,
∴a=3,b=$\frac{13}{4}$.
5a-4b=5×3-4×$\frac{13}{4}$=15-13=2.
点评 本题考查的实数的运算,解题的关键是先将$\sqrt{18}$+$\sqrt{9}$$+\sqrt{\frac{1}{8}}$进行化简合项,得出a、b的值.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列与-2x2y是同类项的是( )
| A. | x2y2 | B. | $\frac{-4x2y}{3}$ | C. | -xy2 | D. | -2xy |
19.若正方形的一条对角线的长为10cm,则此时正方形的面积为( )
| A. | 100cm2 | B. | 75cm2 | C. | 50cm2 | D. | 25cm2 |
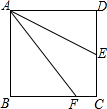 如图,在四边形ABCD中,∠C=∠D=90°,E是CD中点,F是BC上一点,且AE平分∠DAF,求证:AF=AD+CF.
如图,在四边形ABCD中,∠C=∠D=90°,E是CD中点,F是BC上一点,且AE平分∠DAF,求证:AF=AD+CF.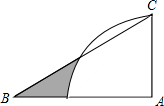 如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)
如图,Rt△ABC中,∠A=90°,∠B=30°,AC=6,以A为圆心,AC长为半径画四分之一圆,则图中阴影部分面积为9$\sqrt{3}$-3π.(结果保留π)