题目内容
求直线 y=2x﹣1 与两坐标轴围成三角形的面积.
【考点】一次函数图象上点的坐标特征.
【分析】根据一次函数的性质,求得函数 y=2x﹣1 的图象与两条坐标轴交点分别是(0,﹣1)和(﹣  ,0),所围成的三角形是直角三角形,利用三角形面积公式,求得三角形的面积.
,0),所围成的三角形是直角三角形,利用三角形面积公式,求得三角形的面积.
【解答】解:根据一次函数的性质,求得函数 y=2x﹣1 的图象与两条坐标轴交点分别是(0,﹣1)
和(﹣ ,0), 即高为 1,底为
,0), 即高为 1,底为 .
.
∴所围成的三角形的面积为:  ×
×  =
=  .
.
【点评】根据一次函数的性质,求得函数 y=2x﹣1 的图象与两条坐标轴交点,即为所求三角形的高 和底,即可求出三角形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
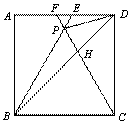 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.
如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.
给出下列结论:①△BDE∽△DPE;②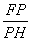 =
= 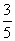 ;
;
③DP2=PH·PB; ④ 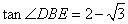 .
.
|
A. ①②③④ B. ①②④ C. ②③④ D. ①③④

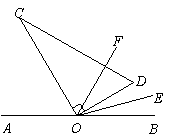 (2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
(2)若OE平分∠BOD,OF平分∠BOC,求∠EOF的度数.
 B.
B.  C.
C.  D.
D. 
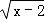 有意义,则 x 的取值范围是( ) A.x<2 B.x≠2 C.x≤2 D.x≥2
有意义,则 x 的取值范围是( ) A.x<2 B.x≠2 C.x≤2 D.x≥2