题目内容
(本小题满分11分)已知关于x的函数y=m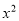 -x-(m-1).
-x-(m-1).
(1)m=__________时,y=m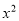 -x-(m-1)是一次函数;
-x-(m-1)是一次函数;
(2)求证:对任何实数m,y=m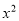 -x-(m-1)的图像与
-x-(m-1)的图像与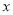 都有公共点;
都有公共点;
(3)若是关于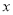 的二次函数y=m
的二次函数y=m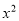 -x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
-x-(m-1)的图像与x有两个不同的公共点A、B (点A在点B左边),图像顶点为C,且△ABC是等腰直角三角形,求m的值;
(4)是否存在这样的点P,使得对任何实数m,y=m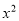 -x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
-x-(m-1)的图像都经过P点?若存在,求出所有P的坐标;若不存在,请说明理由.
(1)m=0;(2)见解析;(3)m=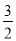 ,或m=-
,或m=- ;(4)(1,0)或(-1,2).
;(4)(1,0)或(-1,2).
【解析】
试题分析:(1)根据一次函数的定义进行求解;(2)分一次函数和二次函数两种情况进行讨论计算;(3)首先求出A、B两点的坐标,然后求出AB的长度以及顶点的纵坐标,根据等腰直角三角形的性质得出AB=2×顶点的纵坐标,求出m的值;(4)首先去m=0和m=1将函数化成简单的一次函数和二次函数,然后求出它们的交点坐标,将交点坐标分别代入解析式,看是否符合解析式,如果符合就是点P.
试题解析:(1)根据题意得:m=0
(2)m=0 时,y=-x+1与x轴交于点(1,0)
M≠0时,△=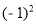 +4m(m-1)=
+4m(m-1)=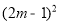 ≥0
≥0
∴对任何实数m,y=m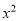 -x-(m-1)的图像与x都有公共点;
-x-(m-1)的图像与x都有公共点;
(3) 由m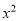 -x-(m-1)=0得
-x-(m-1)=0得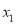 =1,
=1, ∴AB=
∴AB=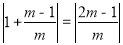
且顶点C的纵坐标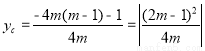
∵△ABC是等腰直角三角形
∴AB=2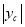 即
即
∴m= 或m=
或m=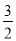 ,或m=-
,或m=-
经检验m=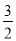 ,或m=-
,或m=-
(4)由m=0得y=-x+1, m=1得y=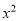 -x
-x
由 解得
解得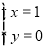 或
或
对任何实数m
当x=1时,y=m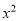 -x-(m-1)=m-1-(m-1)=0
-x-(m-1)=m-1-(m-1)=0
当x=-1时,y=m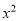 -x-(m-1)=m+1-(m-1)=2
-x-(m-1)=m+1-(m-1)=2
对任何实数m,y=m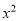 -x-(m-1)的图像都经过点(1,0)(-1,2)
-x-(m-1)的图像都经过点(1,0)(-1,2)
即所求点P的坐标为(1,0)或(-1,2)
考点:二次函数的性质、一次函数的性质、等腰三角形的性质.
考点分析: 考点1:一次函数 函数的定义:一般地,在一个变化过程中,如果有两个自变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
对函数概念的理解,主要抓住以下三点:
①有两个变量;
②一个变量的每一个数值随着另一个变量的数值的变化而变化;
③对于自变量每一个确定的值,函数有且只有一个值与之对应。
例如:y=±x,当x=1时,y有两个对应值,所以y=±x不是函数关系。对于不同的自变量x的取值,y的值可以相同,例如,函数:y=|x|,当x=±1时,y的对应值都是1。 理解函数的概念应扣住下面三点:
(1)函数的概念由三句话组成:“两个变量”,“x的每一个值”,“y有惟一确定的值”;
(2)判断两个变量是否有函数关系不仅看它们之间是否有关系式存在,更重要地是看对于x的每一个确定的值。y是否有惟一确定的值和它对应;(3)函数不是数,它是指某一变化过程中两个变量之间的关系。 函数的表示方法:
(1)解析法:两个变量之间的关系有时可以用含有这两个变量及数学运算符号的等式来表示,这种表示方法叫做解析法.
(2)列表法:把自变量x的一系列值和函数y的对应值列成一个表格来表示函数关系,这种表示方法叫做列表法.
(3)图象法:用图象表示函数关系的方法叫做图象法. 函数的判定:
①判断两个变量是否有函数关系,不仅看他们之间是否有关系式存在,更重要的是看对于x的每个确定的值,y是否有唯一确定的值和他对应。
②函数不是数,他是指某一变化过程中两个变量之间的关系。 考点2:二次函数 定义:
一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 等于( )
等于( )

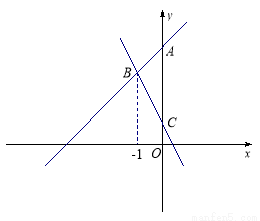
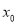 ,0),若-2<
,0),若-2<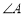 的正切值等于 ( )
的正切值等于 ( )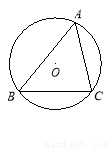
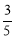 B.
B.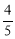 C.
C.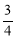 D.
D.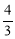
 的大致图象如图所示,关于该二次函数,下列说法错误的是( )
的大致图象如图所示,关于该二次函数,下列说法错误的是( )
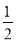
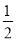 时,y随x的增大而减小
时,y随x的增大而减小