题目内容
如图,在顶角为30°的等腰△ABC中,AB=AC,若过点C作CD⊥AB于点D.根据图形计算tan∠BCD= .
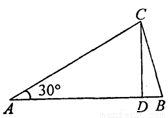
 .
.
【解析】
试题分析:此题可设AB=AC=2x,由已知可求出CD和AD,那么也能求出BD=AB-AD,从而求出tan∠BCD的值.
试题解析:由已知设AB=AC=2x,
∵∠A=30°,CD⊥AB,
∴CD= AC=x,
AC=x,
则AD2=AC2-CD2=(2x)2-x2=3x2,
∴AD= x,
x,
∴BD=AB-AD=2x- x=(2-
x=(2- )x,
)x,
∴tan∠BCD= .
.
考点:解直角三角形.
考点分析: 考点1:解直角三角形 (1)解直角三角形的定义在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.
(2)解直角三角形要用到的关系
①锐角直角的关系:∠A+∠B=90°;
②三边之间的关系:a2+b2=c2;
③边角之间的关系:
sinA=∠A的对边斜边=ac,cosA=∠A的邻边斜边=bc,tanA=∠A的对边∠A的邻边=ab.
(a,b,c分别是∠A、∠B、∠C的对边) 试题属性
- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 -3x+m=0有两个不相等的实数根,则实数m的取值范围为( )
-3x+m=0有两个不相等的实数根,则实数m的取值范围为( ) B、m<
B、m< 上.
上.
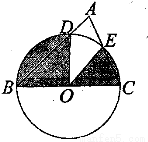
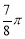 B.
B. C.
C. D.
D.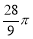
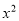 -x-(m-1).
-x-(m-1).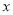 都有公共点;
都有公共点;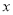 的二次函数y=m
的二次函数y=m