题目内容
如图，把抛物线y=x2沿直线y=x平移
个单位后，其顶点在直线上的A处，则平移后的抛物线解析式是（ ）
A．y=（x+1）2-1
B．y=（x+1）2+1
C．y=（x-1）2+1
D．y=（x-1）2-1
【答案】分析：首先根据A点所在位置设出A点坐标为（m，m）再根据AO=
，利用勾股定理求出m的值，然后根据抛物线平移的性质：左加右减，上加下减可得解析式．
解答：解：∵A在直线y=x上，
∴设A（m，m），
∵OA=
，
∴m2+m2=（
）2，
解得：m=±1（m=-1舍去），
m=1，
∴A（1，1），
∴抛物线解析式为：y=（x-1）2+1，
故选：C．
点评：此题主要考查了二次函数图象的几何变换，关键是求出A点坐标，掌握抛物线平移的性质：左加右减，上加下减．
，利用勾股定理求出m的值，然后根据抛物线平移的性质：左加右减，上加下减可得解析式．解答：解：∵A在直线y=x上，
∴设A（m，m），
∵OA=
，∴m2+m2=（
）2，解得：m=±1（m=-1舍去），
m=1，
∴A（1，1），
∴抛物线解析式为：y=（x-1）2+1，
故选：C．
点评：此题主要考查了二次函数图象的几何变换，关键是求出A点坐标，掌握抛物线平移的性质：左加右减，上加下减．
练习册系列答案
相关题目
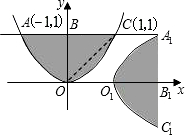如图，把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后，再沿x轴向右平移1个单位得到图形O1A1B1C1，则下列结论错误的是（ ）| A、点O1的坐标是（1，0） | B、点C1的坐标是（2，-1） | C、四边形OBA1B1是矩形 | D、若连接OC，则梯形OCA1B1的面积是3 |
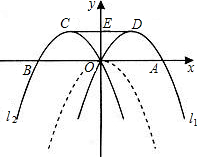标；如果不存在，请说明理由．
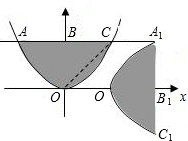如图，把抛物线y=x2与直线y=1围成的图形OABC绕原点O顺时针旋转90°后，再沿x轴向右平移1个单位得到图形O1A1B1C1，则下列结论错误的有（ ）个．
（2012•广安）如图，把抛物线y=
（2012•桂林）如图，把抛物线y=x2沿直线y=x平移