题目内容
如图，过反比例函数
上一点A作AC⊥x轴于C，交函数
的图象于B，若△ABO的面积为4，则k=________．
14
分析：先根据反比例函数系数k的几何意义得出△AOC与△BOC的面积，再根据△ABO的面积为4即可求出k的值．
解答：∵AC⊥x轴，
∴S△AOC=
，S△BOC=
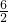=3，
∵反比例函数的图象在第一象限，
∴k＞0，
∴S△AOC=
，
∵S△ABO=S△AOC-S△BOC=-3=4，解得k=14．
故答案为：14．
点评：本题考查的是反比例函数系数k的几何意义，即在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是，且保持不变．
分析：先根据反比例函数系数k的几何意义得出△AOC与△BOC的面积，再根据△ABO的面积为4即可求出k的值．
解答：∵AC⊥x轴，
∴S△AOC=
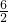，S△BOC==3，∵反比例函数
的图象在第一象限，∴k＞0，
∴S△AOC=
，∵S△ABO=S△AOC-S△BOC=
-3=4，解得k=14．故答案为：14．
点评：本题考查的是反比例函数系数k的几何意义，即在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是
，且保持不变． 
练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
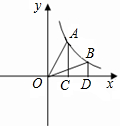如图，过反比例函数y=| 9 |
| x |
| A、S1＞S2 |
| B、S1=S2 |
| C、S1＜S2 |
| D、大小关系不能确定 |
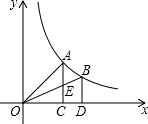如图，过反比例函数y=| 1 |
| x |
| A、S1＞S2 |
| B、S1=S2 |
| C、Sl＜S2 |
| D、大小关系不能确定 |
如图，过反比例函数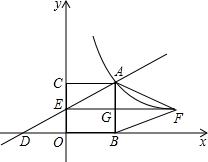
如图，过反比例函数y=