题目内容
15. 某数学活动小组测量了学校旗杆的高度.如图,BC为旗杆,他们先在A点测得C的仰角为45°,再向前走3米到达D点,测得C的仰角为53°,求旗杆高.(结果保留整数)
某数学活动小组测量了学校旗杆的高度.如图,BC为旗杆,他们先在A点测得C的仰角为45°,再向前走3米到达D点,测得C的仰角为53°,求旗杆高.(结果保留整数)参考数据:sin 53°≈0.8,cos 53°≈0.6,tan 37°≈0.75,$\sqrt{2}$≈1.41.
分析 首先根据题意分析图形;本题涉及到两个直角三角形,由三角函数得出AB=x,BD=0.75x,由AB-BD=AD得出方程,解方程即可.
解答 解:设旗杆高BC为x米,
在△ABC中,∠B=90°,∠A=45°,
∴AB=BC=x米,
在△BCD中,∠B=90°,∠BCD=90°-∠BDC=90°-53°=37°,
∴BD=BC•tan37°=0.75 x米,
由题意知:AD=AB-BD,
∴x-0.75x=3,
解得:x=12,
答:旗杆高为12米.
点评 本题考查了解直角三角形的应用-仰角、三角函数;能借助仰角构造直角三角形,由题意列出方程是解决问题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.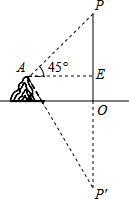 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )| A. | $25\sqrt{3}+75$ | B. | $50\sqrt{3}+50$ | C. | $75\sqrt{3}+75$ | D. | $50\sqrt{3}+100$ |
 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.