Question

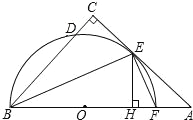
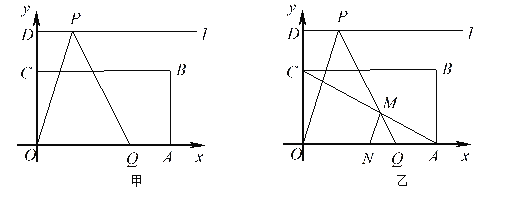
【题目】如图（13），矩形中，、、，射线过点且与轴平行，点、分别是和轴正半轴上动点，满足．

（1）①点的坐标是 ；②= 度；③当点与点重合时，点的坐标为 ；

（2）设的中点为，与线段相交于点，连结，如图（13）乙所示，若为等腰三角形，求点的横坐标；

（3）设点的横坐标为，且，与矩形的重叠部分的面积为，试求与的函数关系式．

Answer 1

【答案】（1）（，）；；（，）；（2）点P的横坐标为m=0或或．(3)见解析.

【解析】分析：(1)、①由四边形OABC是矩形，根据矩形的性质，即可求得点B的坐标：②由正切函数，即可求得∠CAO的度数：③由三角函数的性质，即可求得点P的坐标；(2)、设点的横坐标为，分别根据MN=AN=3，AM=AN和AM=MN三种情况分别求出m的值；(3)、分别从当0≤x≤3时，当3＜x≤5时，当5＜x≤9时，当x＞9时去分析求解即可求得答案．

详解：(1)、（，）；；（，）

(2)、设点的横坐标为，

①当，则，∴，

∵，∴点与重合，点与重合，∴；

②当，作轴、轴，=，

又，∴，解得：m=3﹣；

③当，此时点的横坐标为，过点作⊥于,过作⊥于,

∴，∴，，

∴,，∴,即；

综上所述，点的横坐标为或或；

(3)、当0≤x≤3时，如图1，OI=x，IQ=PItan60°=3，OQ=OI+IQ=3+x；

由题意可知直线l∥BC∥OA， 可得，∴EF=（3+x），

此时重叠部分是梯形，其面积为：

；

当3＜x≤5时，如图2，

当5＜x≤9时，如图3，

当x＞9时，如图4，。

综上所述，S与x的函数关系式为： 。