��Ŀ����
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У���ABC��ֱ�������Σ���ACB��90������A��C������ֱ�ΪA����3��0����C��1��0����BC��![]() AC��
AC��
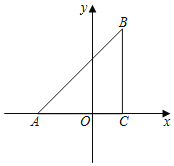
��1����x������һ��D������DB��ʹ����ADB����ABC���ƣ�������ȫ�ȣ��������D�����ꣻ
��2���ڣ�1���������£���P��Q�ֱ���AB��AD�ϵĶ��㣬����PQ����AP��DQ��m�����Ƿ����������m��ʹ����APQ����ADB���ƣ�����ڣ������m��ֵ���粻���ڣ���˵�����ɣ�
���𰸡���1����![]() ��0������2�����ڣ���m��
��0������2�����ڣ���m��![]() ��
��![]() ʱ����APQ����ADB���ƣ����ɼ�����
ʱ����APQ����ADB���ƣ����ɼ�����
��������
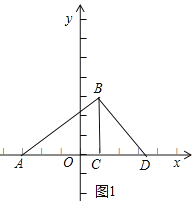
��1����ͼ1������B��BD��AB����x���ڵ�D����֤��ABC�ס�ADB���ɵ���ABC����ADB����֤��ABC�ס�BDC���ɵ�![]() ������CD�ij����������D���ꣻ
������CD�ij����������D���ꣻ
��2��������������ۣ������������ε����ʿ���⣮
��1����ͼ1������B��BD��AB����x���ڵ�D��
�ߡ�A����A����ACB����ABD��90����
���ABC�ס�ADB��
���ABC����ADB���ҡ�ACB����BCD��90����
���ABC�ס�BDC��
��![]()
��A����3��0����C��1��0����
��AC��4��
��BC��![]() AC��
AC��
��BC��3��
��AB��![]() ��
��![]() ��5��
��5��
��![]() ��
��
��![]() ��
��
��CD��![]() ��
��
��AD��AC+CD��4+![]() ��
��![]() ��
��
��OD��AD��AO��![]() ��
��
���D����������![]() ��0����
��0����
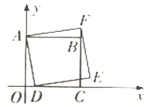
��2����ͼ2������APC����ABD��90��ʱ��
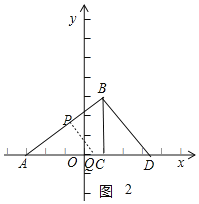
�ߡ�APC����ABD��90������BAD����PAQ��
���APQ�ס�ABD��
��![]() ��
��
��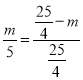
��m��![]() ��
��
��ͼ3������AQP����ABD��90��ʱ��
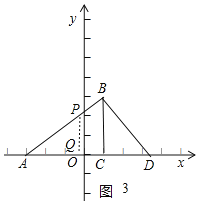
�ߡ�AQP����ABD��90������PAQ����BAD��
���APQ�ס�ADB��
��![]() ��
��
��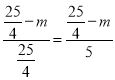
��m��![]() ��
��
������������m��![]() ��
��![]() ʱ����APQ����ADB���ƣ�
ʱ����APQ����ADB���ƣ�

 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�