题目内容
20.若直角三角形的两边长为a、b,且$\sqrt{{a}^{2}-12a+36}$+|b-8|=0,则该直角三角形的斜边长为8或10.分析 任何数的绝对值,以及算术平方根一定是非负数,已知中两个非负数的和是0,则两个一定同时是0;另外已知直角三角形两边a、b的长,分类讨论即可求出斜边长.
解答 解:∵$\sqrt{{a}^{2}-12a+36}$+|b-8|=0,
∴a2-12a+36=(a-6)2=0,b-8=0,
∴a=6,b=8,
分两种情况:
①在直角三角形中,当b为最长边时,斜边长=8;
②在直角三角形中,当a和b为两条直角边长时,
斜边长=$\sqrt{{6}^{2}+{8}^{2}}$=10;
综上所述,该直角三角形的斜边长为8或10;
故答案为:8或10.
点评 本题考查了勾股定理,绝对值、算术平方根的非负性质,考查了分类讨论思想;本题中讨论边长为8的边是直角边还是斜边是解题的关键.

练习册系列答案
相关题目
10.有理数a的相反数是-a,它们之间的大小关系( )
| A. | a>-a | B. | a<-a | C. | a>-a或a=-a | D. | 不能确定 |
15.如果关于x的一元二次方程x2-4x+m=0没有实数根,那么m的取值范围是( )
| A. | m<2 | B. | m>4 | C. | m>16 | D. | m<8 |
12.如图中的线段,直线或射线,能相交的是( )
| A. |  | B. |  | C. |  | D. |  |
 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这跟芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?
在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形.在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这跟芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面.请问这个水池的深度和这根芦苇的长度各为多少?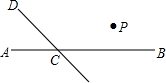 如图,直线CD与直线AB相交于C,根据下列语句画图
如图,直线CD与直线AB相交于C,根据下列语句画图