Question

【题目】如图，四边形与四边形都是正方形.

（1）当正方形绕点在平面内旋转时，与有怎样的数量和位置关系？”并证明你的结论：

（2）若，正方形绕点旋转，当点转到直线上时，恰好是，试问：当点转到直线或直线上时，求的长（本小题画出图形并写出结论，不必写出过程）

Answer 1

【答案】（1）AD=CF且AD⊥CF；（2）+1或-1或2．

【解析】

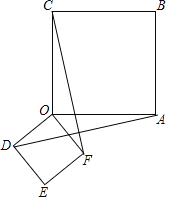
（1）结论：AD=CF且AD⊥CF．如图1中，设CF交OA于K，交AD于J．证明△AOD≌△COF（SAS）即可解决问题．
（2）根据条件首先求出正方形ODEF的边长，分四种情形分别求解即可解决问题．

（1）结论：AD=CF且AD⊥CF．
理由：如图1中，设CF交OA于K，交AD于J．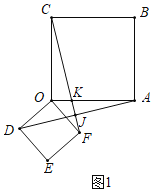

∵四边形OABC与四边形ODEF都是正方形，
∴OA=OC，OD=OF，∠AOC=∠DOF=90°，
∴∠AOD=∠COF，
∴△AOD≌△COF（SAS），
∴AD=CF，∠OCF=∠OAD，
∵∠OCK+∠OKC=90°，∠OKC=∠AKJ，
∴∠AKJ+∠KAJ=90°，
∴∠AJK=90°
∴AD⊥CF．

（2）如图2中，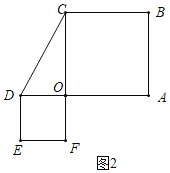

由题意：在Rt△COD中，∠COD=90°，OC=OA= ，∠OCD=30°，
∴OD=OCtan30°==1，
此时AD=1+
如图3中，当点D在CO的延长线上时，AD==2．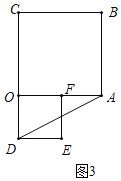

如图4中，当点D在线段OA上时，AD=-1，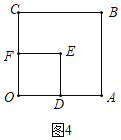

如图5中，当点D在线段OC上时，AD==2，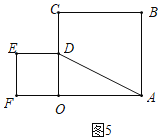

综上所述，满足条件的AD的值为+1或-1或2．