题目内容
已知一个四边形的四边都相等,它的一条对角线长2,一个内角是60°,现分别以这个四边形的两条对角线所在的直线为坐标轴建立直角坐标系,求这个四边形各个顶点的坐标.
考点:坐标与图形性质
专题:数形结合
分析:先根据菱形的判定得到四边形ABCD为菱形,画出直角坐标系,然后分类讨论:当AC=2,∠ABC=60°时;当BD=2,∠ABC=60°时;当AC=2,∠BAD=60°时;当BD=2,∠BAD=60°时,利用菱形的性质和含30度的直角三角形三边的关系求出各种情况下的OA、OB、OC、OD的长,再根据坐标轴上点的坐标特征写出菱形四个顶点的坐标.
解答:解:因为四边形ABCD中,AB=BC=CD=DA,所以四边形ABCD为菱形,
以AC和BD所在的直线为坐标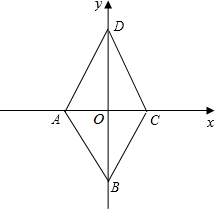 轴建立直角坐标系,如图,
轴建立直角坐标系,如图,
当AC=2,∠ABC=60°时,则OA=OC=1,
∠ABO=
∠ABC=30°,则OB=
OA=
,
所以A(-1,0),B(0,-
),C(1,0),D(0,
),
当BD=2,∠ABC=60°时,则OB=OD=1,
∠ABO=
∠ABC=30°,则OA=
OB=
,
所以A(-
,0),B(0,-1),C(
,0),D(0,1),
当AC=2,∠BAD=60°时,则OA=OC=1,
∠DAO=
∠DAB=30°,则OD=
OA=
,
所以A(-1,0),B(0,-
),C(1,0),D(0,
),
当BD=2,∠BAD=60°时,则OB=OD=1,
∠DAO=
∠DAB=30°,则OA=
OD=
,
所以A(-
,0),B(0,-1),C(
,0),D(0,1).
以AC和BD所在的直线为坐标
 轴建立直角坐标系,如图,
轴建立直角坐标系,如图,当AC=2,∠ABC=60°时,则OA=OC=1,
∠ABO=
| 1 |
| 2 |
| 3 |
| 3 |
所以A(-1,0),B(0,-
| 3 |
| 3 |
当BD=2,∠ABC=60°时,则OB=OD=1,
∠ABO=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
所以A(-
| ||
| 3 |
| ||
| 3 |
当AC=2,∠BAD=60°时,则OA=OC=1,
∠DAO=
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
所以A(-1,0),B(0,-
| ||
| 3 |
| ||
| 3 |
当BD=2,∠BAD=60°时,则OB=OD=1,
∠DAO=
| 1 |
| 2 |
| 3 |
| 3 |
所以A(-
| 3 |
| 3 |
点评:本题考查了坐标与图形性质:利用点的坐标求线段的长和判断线段与坐标轴的位置关系.也考查了菱形的性质.

练习册系列答案
相关题目
下列各式计算正确的是( )
| A、x4•x2=x8 |
| B、(x4y3)2=x4y5 |
| C、6x2•3xy=18x3y |
| D、a4+a7=a11 |
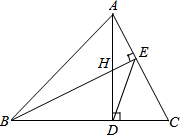 如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:
如图所示,△ABC的高AD、BE相交于点H,若BH=AC,则下列结论:①AE=CE;②∠ABC=45°;③DH=DC;④∠CED=45°
成立的有( )
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
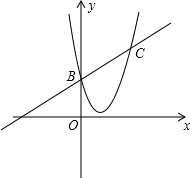 如图,在平面直角坐标系中,一次函数y=
如图,在平面直角坐标系中,一次函数y=