题目内容
 如图,在等边△ABC中,D、E、F分别是BC,AC,AB上的点,且DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的面积之比等于
如图,在等边△ABC中,D、E、F分别是BC,AC,AB上的点,且DE⊥AC,EF⊥AB,FD⊥BC,则△DEF与△ABC的面积之比等于
- A.1:3
- B.2:3
- C.
 :2
:2 - D.
 :3
:3
A
分析:三角形的面积= ×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.
×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.
解答:∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠C+∠EDC=90°,∠FDE+∠EDC=90°,
∴∠C=∠FDE ,
,
同理可得:∠B=∠DFE,∠A=DEF,
∴△DEF∽△CAB,
∴△DEF与△ABC的面积之比=( )2,
)2,
又∵△ABC为正三角形,
∴∠B=∠C=∠A=60°,△EFD是等边三角形,
∴EF=DE=DF,
又∵DE⊥AC,EF⊥AB,FD⊥BC,
∴△AEF≌△CDE≌△BFD,
∴BF=AE=CD,AF=BD=DC,
在Rt△DEC中,
DE=DC×sin∠C= DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC= DC,
DC,
又∵DC+BD=BC=AC= DC,
DC,
∴ =
= =
= ,
,
∴△DEF与△ABC的面积之比等于:( )2=
)2= =1:3.
=1:3.
故选:A.
点评:本题主要考查如何求三角形的面积之比,若能证出两个三角形是相似三角形,此时三角形的面积之比等于对应边之比的平方,只要求出对应边比即可.
分析:三角形的面积=
 ×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.
×高×底,所以相似三角形的面积之比等于边之比的平方,由DE⊥AC,EF⊥AB,FC⊥BC得出△DEF与△ABC的角对应相等,即:△DEF∽△CAB,求出两个三角形的边之比即可,又知△ABC是正三角形,所以∠B=∠C=∠A=60°,利用余弦和正弦定理求出两个三角形的边之比.解答:∵DE⊥AC,EF⊥AB,FD⊥BC,
∴∠C+∠EDC=90°,∠FDE+∠EDC=90°,
∴∠C=∠FDE
 ,
,同理可得:∠B=∠DFE,∠A=DEF,
∴△DEF∽△CAB,
∴△DEF与△ABC的面积之比=(
 )2,
)2,又∵△ABC为正三角形,
∴∠B=∠C=∠A=60°,△EFD是等边三角形,
∴EF=DE=DF,
又∵DE⊥AC,EF⊥AB,FD⊥BC,
∴△AEF≌△CDE≌△BFD,
∴BF=AE=CD,AF=BD=DC,
在Rt△DEC中,
DE=DC×sin∠C=
 DC,EC=cos∠C×DC=
DC,EC=cos∠C×DC= DC,
DC,又∵DC+BD=BC=AC=
 DC,
DC,∴
 =
= =
= ,
,∴△DEF与△ABC的面积之比等于:(
 )2=
)2= =1:3.
=1:3.故选:A.
点评:本题主要考查如何求三角形的面积之比,若能证出两个三角形是相似三角形,此时三角形的面积之比等于对应边之比的平方,只要求出对应边比即可.

练习册系列答案
相关题目
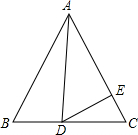 如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )
如图,在等边△ABC中,D为BC边上一点,E为AC边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC的面积为( )A、81
| ||||
B、
| ||||
C、
| ||||
D、
|
 16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是
16、如图,在等边△ABC的边BC上任取一点D,作∠ADE=60°,DE交∠C的外角平分线于E,则△ADE是 21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°.
21、如图,在等边△ABC中,AD是∠BAC的平分线,点E在AC边上,且∠EDC=15°. 如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm.
如图,在等边△ABC中,D是AC的中点,延长BC到点E,使CE=CD,AB=10cm. 如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证:
如图,在等边△ABC中,BF是高,D是BF上一点,且OF=AF,作OE⊥BF,垂足为D,且OE=OB,连AE、AO、BE,求证: