题目内容
9．
如图所示，?ABCD的面积为20$\sqrt{5}$，∠B=30°，若BC=8$\sqrt{5}$，求?ABCD的周长．
分析 由平行四边形的面积以及BC的长，可求出AE的长，再由∠B=30°，即可求出AB的长，进而可求出?ABCD的周长．
解答 
解：过点A作AE⊥BC于E，
∵?ABCD的面积为20$\sqrt{5}$，AE⊥BC于E点，BC=8$\sqrt{5}$，
∴AE=20$\sqrt{5}$÷8$\sqrt{5}$=$\frac{5}{2}$，
∵∠B=30°，
∴AB=5，
∴?ABCD的周长=2（AB+BC）=2×（5+8$\sqrt{5}$）=10+16$\sqrt{5}$．
点评 此题考查了平行四边形的性质以及含30°角的直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
如图，已知矩形ABCD，AD=2，CD=5，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．
某中学为了提高学生羽毛球水平，准备将一块周长为76m的长方形空地，设计成长、宽分别相等的9块长方形羽毛球场（如图），新建的羽毛球场需要进行装修，已知装修费用为每平方分米1元，问学校要投资多少钱来装修？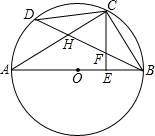
如图，AB是⊙O的直径，C是$\widehat{BD}$的中点，CE⊥AB于E，BD交CE于点F，BD交CA于点H．
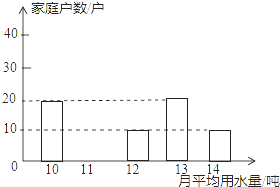自来水公司对某社区600户居民家庭的用水情况做了一次调查．调查小组随机抽查了其中的100户家庭一年的月平均用电量（单位：吨），并将调查结果制成了如图所示的条形统计图．