Question

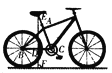
【题目】如图所示的是一辆自行车的侧面示意图．已知车轮直径为65 cm，车架中AC的长为42 cm，座杆AE的长为18 cm，点E，A，C在同一条直线上，后轴轴心B与中轴轴心C所在直线BC与地面平行，∠C＝73°，求车座E到地面的距离EF．(结果精确到l cm，参考数据：sin 73°≈0.96，cos 73°≈0.29，tan 73°≈3.27)

Answer 1

【答案】90

【解析】试题分析：如图所示，题中所求线段是EF，而DF=0.5×65=32.5为已知，所以只需求出ED，而ED在直角三角形ECD中，且∠C=73°为已知，斜边EC=60为已知，所以可用正弦的概念求出ED=60×sin73°≈60×0.96≈57.6，再加上32.5即EF的长约为90cm．

试题解析：如图，在Rt△EDC中，

CE=AE＋AC=18＋42=60(cm)．

∵sin C=，

∴DE=CEsin C=60×sin73°≈60×0.96=57.6(cm)．

又∵DF=×65=32.5(cm)，

∴EF=DE＋DF≈57.6＋32.5≈90(cm)．

即车座E到地面的距离EF约为90cm．