Question

【题目】如图，已知直线l：y＝2x＋4交x轴于A，交y轴于B．

(1) 直接写出直线l向右平移2个单位得到的直线l1的解析式_______；

(2) 直接写出直线l关于y＝－x对称的直线l2的解析式_______；

(3) 点P在直线l上，若S△OAP＝2S△OBP，求P点坐标．

Answer 1

【答案】（1）；（2）；（3）点P的坐标为或．

【解析】

（1）根据一次函数的图象平移规律即可得；

（2）先求出点A、B的坐标，再求出点A、B关于对称点的坐标，然后利用待定系数法求解即可得；

（3）设点P的坐标为，分点P在直线第一象限的图象上、点P在直线第二象限的图象上、点P在直线第三象限的图象上，再根据，利用三角形的面积公式列出等式求解即可得．

（1）一次函数的图象平移规律：向左（或向右）平移a个单位长度得到的函数解析式为（或）；向上（或向下）平移a个单位长度得到的函数解析式为（或）

则直线向右平移2个单位得到的直线的解析式为，即

故答案为：；

（2）对于

当时，，解得，则

当时，，则

由对称性可知，点关于直线对称点坐标为；点关于直线对称点坐标为

设直线的解析式为

将点，代入得：，解得

则直线的解析式为

故答案为：；

（3）设点P的坐标为

因为点P在直线上，则分以下三种情况：

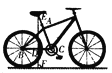
①如图1，点P位于直线第一象限的图象上

则有，解得

过点P作轴于点C，作轴于点D

则

由得：，解得（符合题设）

此时，点P的坐标为

②如图2，点P位于直线第二象限的图象上

则有，解得

过点P作轴于点C，作轴于点D

则

由得：，解得（符合题设）

此时，点P的坐标为

③如图3，点P位于直线第三象限的图象上

此时，不可能存在点P，使得

综上，点P的坐标为或．