题目内容
如图，已知⊙O中，∠AOB的度数为80°，C是圆周上一点，则∠ACB的度数为
- A.50°
- B.80°
- C.280°
- D.140°
D
分析：在优弧AB上任意找一点D，连接AD，BD，根据圆周角定理求得∠D的度数，再根据圆内接四边形的对角互补求得∠ACB的度数．
解答：
解：在优弧AB上任意找一点D，连接AD，BD
∵∠D=
∠AOB=40°
∴∠ACB=180°-40°=140°．
故选D．
点评：考查了圆周角定理和圆内接四边形的性质的运用．
分析：在优弧AB上任意找一点D，连接AD，BD，根据圆周角定理求得∠D的度数，再根据圆内接四边形的对角互补求得∠ACB的度数．
解答：
解：在优弧AB上任意找一点D，连接AD，BD∵∠D=
∠AOB=40°∴∠ACB=180°-40°=140°．
故选D．
点评：考查了圆周角定理和圆内接四边形的性质的运用．
练习册系列答案
期末集结号系列答案
相关题目
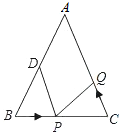如图，已知△ABC中，AB=AC=10cm，BC=8cm，点D为AB的中点．
29、如图，已知△ABC中，AD⊥BC于D，AD=BD，DC=DE．求证：∠C=∠1．
34、如图，已知△ABC中，AB=AC，AB的垂直平分线交AB于D，交AC于E，若△ABC与△EBC的周长分别是26cm、18cm，则AC=
如图，已知△ABC中，AD=DB，D、E分别为BC、AB上一点，连接DE，∠1=∠2．
如图，已知△ABC中，AB＞AC，BE、CF都是△ABC的高，P是BE上一点且BP=AC，Q是CF延长线上一点且CQ=AB，连接AP、AQ、QP，求证：