题目内容
 如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.
如图,已知△ABC中,AD=DB,D、E分别为BC、AB上一点,连接DE,∠1=∠2.(1)求证:△ABC∽△EAD;
(2)若AE=3,AD=4,BC=6,求BE的长.
分析:(1)由AD=DB,可得∠B=∠BAD,又由∠1=∠2,易证得∠AED=∠BAC,则可根据有两角对应相等的三角形相似,证得△ABC∽△EAD;
(2)由△ABC∽△EAD,根据相似三角形的对应边成比例,即可求得AB的长,继而可求得BE的长.
(2)由△ABC∽△EAD,根据相似三角形的对应边成比例,即可求得AB的长,继而可求得BE的长.
解答:(1)证明:∵AD=DB,
∴∠B=∠BAD,
∵∠1=∠2,∠AED=∠B+∠2,∠BAC=∠BAD+∠1,
∴∠AED=∠BAC,
∴△ABC∽△EAD;
(2)∵△ABC∽△EAD,
∴
=
,
∵AE=3,AD=4,BC=6,
∴
=
,
解得:AB=
,
∴BE=AB-AE=
-3=
.
∴∠B=∠BAD,
∵∠1=∠2,∠AED=∠B+∠2,∠BAC=∠BAD+∠1,
∴∠AED=∠BAC,
∴△ABC∽△EAD;
(2)∵△ABC∽△EAD,
∴
| AB |
| AE |
| BC |
| AD |
∵AE=3,AD=4,BC=6,
∴
| AB |
| 3 |
| 6 |
| 4 |
解得:AB=
| 9 |
| 2 |
∴BE=AB-AE=
| 9 |
| 2 |
| 3 |
| 2 |
点评:此题考查了相似三角形的判定与性质以及等腰三角形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.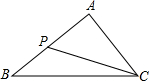 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )