题目内容
16.若|x|=4,$\sqrt{{y}^{2}}$=9,|x-y|=x-y,则x+y的值为( )| A. | 5或13 | B. | -5或-13 | C. | -5或13 | D. | 5或-13 |
分析 根据绝对值的性质,二次根式的性质,可得x、y的值,根据有理数的加法,可得答案.
解答 解:由|x|=4,$\sqrt{{y}^{2}}$=9,|x-y|=x-y,得
x=4,或x=-4,y=-9.
x+y=4+(-9)=-5,
x+y=-4+(-9)=-13,
故选:B.
点评 本题考查了实数的性质,利用绝对值的性质,二次根式的性质得出x、y的值是解题关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
11.下列叙述正确的是( )
| A. | 有理数中有最大的数 | B. | 零是整数中最小的数 | ||
| C. | 有理数中有绝对值最小的数 | D. | 任何数的绝对值一定是正数 |
6.-(-3)、-(+2)的化简结果为( )
| A. | -3、-2 | B. | 3、-2 | C. | -3、2 | D. | 3、2 |
 若用A、B、C、D分别表示有理数a、b、c,0为原点如图所示.已知a<c<0,b>0.
若用A、B、C、D分别表示有理数a、b、c,0为原点如图所示.已知a<c<0,b>0.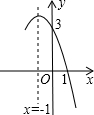 抛物线y=-x2+bx+c的部分图象如图所示,则-x2+bx+c>0的解集是-3<x<1.
抛物线y=-x2+bx+c的部分图象如图所示,则-x2+bx+c>0的解集是-3<x<1.