题目内容
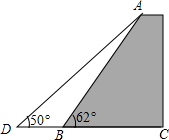 2014年12月31日晚23时35分许,上海外滩陈毅广场发生拥挤踩踏事故.为了排除安全隐患,因此无锡市政府决定改造蠡湖公园的一处观景平台.如图,一平台的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使平台更加牢固,欲改变平台的坡面,使得坡面的坡角∠ADB=50°,则此时应将平台底部向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
2014年12月31日晚23时35分许,上海外滩陈毅广场发生拥挤踩踏事故.为了排除安全隐患,因此无锡市政府决定改造蠡湖公园的一处观景平台.如图,一平台的坡角∠ABC=62°,坡面长度AB=25米(图为横截面),为了使平台更加牢固,欲改变平台的坡面,使得坡面的坡角∠ADB=50°,则此时应将平台底部向外拓宽多少米?(结果保留到0.01米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)考点:解直角三角形的应用-坡度坡角问题
专题:
分析:过A点作AE⊥CD于E,在Rt△ABE中,根据∠ABE=62°,求出AE、BE的长度,然后在Rt△ADE中,求出DE的长度,继而可求得BD的长度.
解答:解:过A点作AE⊥CD于E.
在Rt△ABE中,
∵∠ABE=62°,
∴AE=AB•sin62°=25×0.88=22米,
BE=AB•cos62°=25×0.47=11.75米,
在Rt△ADE中,∠ADB=50°,
∴DE=
=
,
∴DB=DC-BE≈6.58米.
答:向外拓宽大约6.58米.

在Rt△ABE中,
∵∠ABE=62°,
∴AE=AB•sin62°=25×0.88=22米,
BE=AB•cos62°=25×0.47=11.75米,
在Rt△ADE中,∠ADB=50°,
∴DE=
| AE |
| tan50° |
| 55 |
| 3 |
∴DB=DC-BE≈6.58米.
答:向外拓宽大约6.58米.
点评:本题考查了解直角三角形的应用,解答本题的关键是根据所给的坡角构造直角三角形,利用三角函数的知识求解.

练习册系列答案
相关题目
下列各组数中互为相反数的是( )
| A、+(+5)与-(-5) | ||
| B、+(-5)与-(+5) | ||
C、+(+5)与-(-
| ||
| D、+(-5)与-(-5) |
 在同一平面直角坐标系内画出直线y1=-x+4和y2=2x-5的图象,结合图象求:
在同一平面直角坐标系内画出直线y1=-x+4和y2=2x-5的图象,结合图象求: 已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC.
已知,如图,DE⊥AC,BF⊥AC,AD=CB,DE=BF,求证:AB∥DC. 如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是
如图,已知在平行四边形ABCD中,AB=4,BC=6,AD到BC的距离AE=2,则AB到CD的距离AF的长是