题目内容
2.已知方程3x2+2x-3=0的两根x1、x2,求下列代数式的值:(x1+x2=-$\frac{b}{a}$,x1•x2=$\frac{c}{a}$)(1)x12+x22;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$.
分析 先根据根与系数的关系,求出两根之积与两根之和的值;然后将代数式变形为两根之和与两根之积的形式,
(1)x12+x22=(x1+x2)2-2x1x2;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$;
最后代入数值进行计算.
解答 解:∵方程3x2+2x-3=0的两根x1、x2,
∴x1+x2=-$\frac{2}{3}$,x1•x2=-1;
(1)x12+x22=(x1+x2)2-2x1x2=$\frac{22}{9}$;
(2)$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{2}{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.正比例函数y=kx(k≠0)经过不同象限的两点A(2,m),B(n,3),则一定成立的有( )
| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n<0 | D. | m<0,n>0 |
17.已知x=4是方程x2-a2=0的一个根,则方程的另一个根是( )
| A. | -4 | B. | 4 | C. | -16 | D. | 16 |
14.下列各图中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
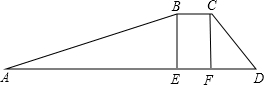 如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.
如图所示,拦水坝的横断面为梯形ABCD,斜坡AB的坡度为$\frac{1}{2.5}$,坝顶宽BC=2.8,坝高BE=4.2米,斜坡CD=7.5米.