Question

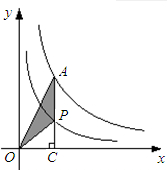
如图，反比例函数图象与一次函数图象交于A，B两点．
（1）求反比例函数的解析式；
（2）连接OA，OB，当△AOB的面积为

15

2

时，求直线AB的解析式．

Answer 1

（1）设函数解析式为y=

k

x

，
将A（1，4）代入解析式得：k=1×4=4，
所以函数解析式为y=

4

x

．

（2）作AD⊥BD．
设B点坐标为（x，y），
于是S_△ABD-S_{四边形OFDE}-S_△AOE-S_△BOF=S_△AOB，
所以（-x+1）（-y+4）×

1

2

-[1×（-y）]-2-2=

15

2

，整理得xy-4x+y=19，
与y=

4

x

组成方程组得：

xy-4x+y=19 y= 4 x

，
解得

x=-4 y=-1

．
故B（-4，-1）．
设一次函数解析式为y=kx+b，将A、B点坐标代入解析式得

k+b=4 -4k+b=-1

，
解得函数解析式为y=x+3．