题目内容

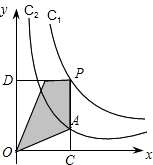
如图，在直角坐标系xOy的第一象限内，一次函数y=k1x+b（k1≠0）图象与反比例函数y=
k2
x
（k2≠0）的图象交于A（1，4）、B（3，u）两点．
（1）求一次函数的关系式，
（2）当x＞0时，写出不等式
k2
x
＞k1+b的解集．
（1）把A（1，4）代入y=
k2
x
（k2≠0）得k2=1×4=4，
所以反比例函数解析式为y=
4
x
；
把B（3，u）代入y=
4
x
得3u=4，解得u=
4
3
，
所以B点坐标为（3，
4
3
）；
把A（1，4）、B（3，u）代入y=k1x+b（k1≠0）得
k1+b=4
3k1+b=
4
3
，解得
k1=-
4
3
b=
16
3

所以一次函数的解析式为y=-
4
3
x+
16
3
；
（2）0＜x＜1或x＞3．
练习册系列答案
相关题目
如图，反比例函数图象与一次函数图象交于A，B两点．
（1）求反比例函数的解析式；
（2）连接OA，OB，当△AOB的面积为
15
2
时，求直线AB的解析式．
如图所示，P是反比例函数y=
k
x
图象上一点，过P分别向x轴、y轴引垂线，若S阴=3，则解析式为______．
已知双曲线y=
k
x
经过点（-1，3），如果A（a1，b1），B（a2，b2）两点在该双曲线上，且a1＜a2＜0，那么b1______b2．
如图，两个反比例函数y=
k1
x
和y=
k2
x
（其中k1＞k2＞0）在第一象限内的图象依次是C1和C2，设点P在C1上，PC⊥x轴于点C，交C2于点A，PD⊥y轴于点D，交C2于点B，则四边形PAOB的面积为______．
如图，A、B分别是反比例函数y=
10
x
，y=
6
x
图象上的点，过A、B作x轴的垂线，垂足分别为C、D，连接OB、OA，OA交BD于E点，△BOE的面积为S1，四边形ACDE的面积为S2，则S2-S1=______．
如图，已知点C为反比例函数y=-
6
x
上的一点，连结C0并延长交双曲线的另一个分支于D点，过C点向y轴引垂线，过D点向x轴引垂线，两直线相交于E点，那么△CDE的面积为______．
点P，Q在y=-
3
x
的图象上．
（1）若P（1，a），Q（2，b），比较a，b的大小；
（2）若P（-1，a），Q（-2，b），比较a，b的大小；
（3）你能从中发现y随x增大时的变化规律吗？
（4）若P（x1，y1），Q（x2，y2），x1＜x2，你能比较y1与y2的大小吗？
函数y=
k
x
的图象经过点（1，-2），则k的值是（　　）
A．
1
2
B．-
1
2
C．-2D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网