题目内容
17.计算:(1)$\sqrt{12}$-2$\sqrt{1\frac{1}{3}}$-$\sqrt{27}$
(2)$\sqrt{5}$(1+$\sqrt{5}$)-$\sqrt{(-5)^{2}}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先根据二次根式的乘法法则和二次根式的性质运算,然后合并即可.
解答 解:(1)原式=2$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$-3$\sqrt{3}$
=-$\frac{7\sqrt{3}}{3}$;
(2)原式=$\sqrt{5}$+5-5
=$\sqrt{5}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
7. 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
 如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )
如图,?ABCD的周长是22cm,△ABC的周长是17cm,则AC的长为( )| A. | 5 cm | B. | 6 cm | C. | 7 cm | D. | 8 cm |
5.下列计算正确的是( )
| A. | 2a5+a5=2a10 | B. | ${a^{-2}}•{a^{-3}}=\frac{1}{a^6}$ | C. | [(-a)3]2=(-a)6=a6 | D. | a5÷a5=a5-5=a0=0 |
9.绝对值不大于2的整数有( )个.
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
7. 将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
 将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )
将一副三角板按如图方式摆放在一起,若∠2=30°15',则∠1的度数等于( )| A. | 59.45° | B. | 60°15' | C. | 59°75' | D. | 59.75° |
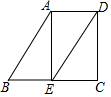 如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.