Question

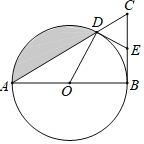
【题目】如图，点D是等边△ABC中BC边的延长线上一点，且AC＝CD，以AB为直径作⊙O，分别交边AC、BC于点E、点F

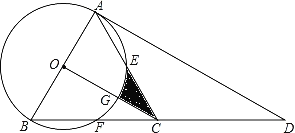
（1）求证：AD是⊙O的切线；

（2）连接OC，交⊙O于点G，若AB＝4，求线段CE、CG与围成的阴影部分的面积S．

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）已知AB为直径，只需证明∠BAD=90°即可，根据直角三角形判定定理证明△ABD为直角三角形即可求出∠DAB＝90°，根据切线的判定推出即可．

（2）连接OE，分别求出△AOE、△AOC，扇形OEG的面积，即可求出答案．

（1）∵△ABC为等边三角形，

∴AC＝BC，

又∵AC＝CD，

∴AC＝BC＝CD，

∴△ABD为直角三角形，

∴AB⊥AD，

∵AB为直径，

∴AD是⊙O的切线．

（2）连接OE，如下图所示：

∵OA＝OE，∠BAC＝60°，

∴△OAE是等边三角形，

∴∠AOE＝60°，

∵CB＝BA，OA＝OB，

∴CO⊥AB，

∴∠AOC＝90°，

∴∠EOC＝30°，

∵△ABC是边长为4的等边三角形，

∴AO＝2，由勾股定理得：OC＝，同理等边△AOE高是，

S阴影＝S△AOC﹣S等边△AOE﹣S扇形EOG．