题目内容
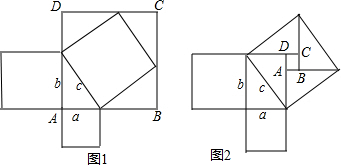
6.为了计算图中大正方形的面积,小明对这个大正方形适当割补后得到图1图2(1)将所有三角形和正方形的面积用a,b,c的关系表示出来;
(2)图1,图2中正方形ABCD的面积分别是多少?你们有哪些表示方式?与同伴进行交流;
(3)你能分别利用图1图2验证勾股定理吗?
分析 (1)利用三角形和正方形的面积公式进行计算;
(2)利用“分割法”进行解答;
(3)根据图形间的面积相等列出等式即可得到勾股定理.
解答 解:(1)如图1,所有三角形的面积都是$\frac{1}{2}$ab,所有正方形的面积分别是b2,a2,(a+b)2;
如图2,所有三角形的面积都是$\frac{1}{2}$ab,所有正方形的面积分别是b2,a2,(a-b)2;
(2)图1中正方形ABCD的面积是(a+b)2,又可以表示为:c2+2ab,
图2中正方形ABCD的面积为(a-b)2,又可以表示为:c2-2ab;
(3)∵图1中正方形ABCD的面积是(a+b)2,又可以表示为:c2+2ab,
∴(a+b)2=c2+2ab,
即a2+b2=c2;
∵图2中正方形ABCD的面积为(a-b)2,又可以表示为:c2-2ab,
∴(a-b)2=c2-2ab,
∴a2+b2=c2,
即直角三角形的两直角边a、b的平方和等于斜边c的平方.
点评 本题考查了勾股定理的几何解释,利用不同的方法表示出大正方形的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14. 如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
 如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )
如图,在?ABCD中,对角线AC、BD交于点O,点E是BC的中点.若OE=3cm,则AB的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
 如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形.
如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画三角形和平行四边形. 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.