题目内容
如图，E、F分别在AD、BC上，EFCD是正方形，且矩形ABCD∽矩形AEFB，则AB：BC的值是________．
1：
分析：根据相似多边形对应边的比相等，设出原来矩形的长与宽，就可得到一个方程，解方程即可求得．
解答：根据条件可知：矩形AEFB∽矩形ABCD．
∴
．
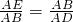设AD=x，AB=y，则AE=x-y．
∴x：y=1：
．
即原矩形长与宽的比为1：．
故答案为：1：．
点评：考查了相似多边形的性质，根据相似形的对应边的比相等，把几何问题转化为方程问题，正确分清对应边，以及正确解方程是解决本题的关键．
分析：根据相似多边形对应边的比相等，设出原来矩形的长与宽，就可得到一个方程，解方程即可求得．
解答：根据条件可知：矩形AEFB∽矩形ABCD．
∴
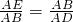．设AD=x，AB=y，则AE=x-y．
∴x：y=1：
．即原矩形长与宽的比为1：
．故答案为：1：
．点评：考查了相似多边形的性质，根据相似形的对应边的比相等，把几何问题转化为方程问题，正确分清对应边，以及正确解方程是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
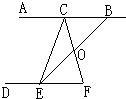28、如图，C、E分别在AB、DF上，小华想知道∠ACE和∠DEC是否互补，但是他有没有带量角器，只带了一副三角尺，于是他想了这样一个办法：首先连接CF，再找出CF的中点O，然后连接EO并延长EO和直线AB相交于点B，经过测量，他发现EO=BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC=EF．以下是他的想法，请你填上根据．
如图，D、E分别在AC、BC的延长线上，且
如图，B、C分别在反比例函数
已知：如图，D、E分别在AB、AC上，若AB=AC，AD=AE，∠A=60°，∠B=35°，则∠BDC的度数是（ ）