题目内容
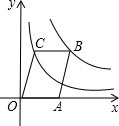如图，B、C分别在反比例函数y=| 4 |
| x |
| 1 |
| x |
3
3
．分析：首先设C（a，b），B（x，b），根据反比例函数关系式求出a与x的关系，从而得到CB=AO的长，再利用平行四边形面积公式算出面积即可．
解答：
解：过C作CE⊥x轴于点E，
设C（a，b），B（x，b），
∵点C在反比例函数y=
上，点B在反比例函数y=
上，
∴ab=1，xb=4，
∴x=4a，
∴CB=4a-a=3a，
∵四边形OABC是平行四边形，
∴AO=CB=3a，
∴四边形OABC的面积是：AO•CE=3ab=3，
故答案为：3．
解：过C作CE⊥x轴于点E，设C（a，b），B（x，b），
∵点C在反比例函数y=
| 1 |
| x |
| 4 |
| x |
∴ab=1，xb=4，
∴x=4a，
∴CB=4a-a=3a，
∵四边形OABC是平行四边形，
∴AO=CB=3a，
∴四边形OABC的面积是：AO•CE=3ab=3，
故答案为：3．
点评：此题主要考查了反比例函数，关键是利用反比例函数关系式表示出C、B两点的坐标，求出AO的长．
练习册系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
11、如图，在锐角△ABC内有一点P，直线AP，BP，CP分别交对边于Q1，Q2，Q3，且∠PQ1C=∠PQ2A=∠PQ3B．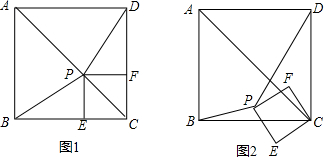
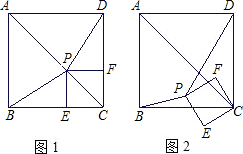的过程中，△PBD的面积是否存在最大值、最小值？如果存在，试求出最大值、最小值；如果不存在，请说明理由．
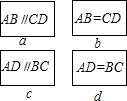小亮同学为了巩固自己对平行四边形判定知识的掌握情况，设计了一个游戏，他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上，卡片如图：