题目内容
 对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被这个圆所覆盖.例如,图中的三角形被一个圆所覆盖.回答问题:
对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被这个圆所覆盖.例如,图中的三角形被一个圆所覆盖.回答问题:(1)边长为1cm的正方形被一个半径为r的圆所覆盖,r的最小值是多少?
(2)边长为1cm的正三角形被一个半径为r的圆所覆盖,r的最小值是多少?
(3)半径为1cm的圆被边长为a的正方形所覆盖,a的最小值是多少?
(4)半径为1cm的圆被边长为a的正三角形所覆盖,a的最小值是多少?
分析:(1)边长为1cm的正方形被一个半径为r的圆所覆盖,求圆的半径,实质上时求边长为1的正方形外接圆的半径,根据题意画出图形,连接正方形外接圆的圆心与两端点的连线,求出正方形一条边所对圆心角的度数,利用勾股定理即可求出r的值;
(2)边长为1cm的正三角形被一个半径为r的圆所覆盖,求r的最小值即求此正三角形外接圆的半径,根据题意画出图形,作出辅助线,垂径定理及锐角三角函数的定义即可解答;
(3)半径为1cm的圆被边长为a的正方形所覆盖,求a的最小值,实际上是求圆的外接正方形的边长,根据题意画出图形,根据勾股定理及正方形的性质即可求解;
(4)半径为1cm的圆被边长为a的正三角形所覆盖,a的最小值,实际上是求边长为1的圆的外切正三角形的面积,根据题意画出图形,利用锐角三角函数的定义即可求解.
(2)边长为1cm的正三角形被一个半径为r的圆所覆盖,求r的最小值即求此正三角形外接圆的半径,根据题意画出图形,作出辅助线,垂径定理及锐角三角函数的定义即可解答;
(3)半径为1cm的圆被边长为a的正方形所覆盖,求a的最小值,实际上是求圆的外接正方形的边长,根据题意画出图形,根据勾股定理及正方形的性质即可求解;
(4)半径为1cm的圆被边长为a的正三角形所覆盖,a的最小值,实际上是求边长为1的圆的外切正三角形的面积,根据题意画出图形,利用锐角三角函数的定义即可求解.
解答: 解:(1)如图(1)所示,
解:(1)如图(1)所示,
连接OB、OC,则∠BOC=
=90°,
∵OB=OC=r,
∴△OBC是等腰直角三角形,
∴OB2+OC2=BC2,即r2+r2=12,
∴r=
;
(2)如图(2)所示,连接OA、OB,过O作OD⊥AB,则AD=
AB=
,
∵△ABC是等边三角形,
∴∠AOB=2∠ACB=2×60°=120°,
∵OD⊥AB,
∴∠AOD=60°,∠OAC=30°,
∴OA=r=
=
=
;
(3)如图(3)所示,连接OA、OE,则OE=r,
∵四边形ABCD是正方形,
∴∠OAE=∠AOE=45°,
∴OE=AE=1,
∴AB=2;
(4)如图(4),连接OB,OD,
∵O是切点,
∴OD⊥BC,OD=1,BD=
,
∵O是△ABC的内心,
∴∠OBD=30°,
∴OD=BD•tan∠OBD=
•
=1,
∴a=2
.
故答案为:
,
,2,2
.
 解:(1)如图(1)所示,
解:(1)如图(1)所示,连接OB、OC,则∠BOC=
| 360° |
| 4 |
∵OB=OC=r,
∴△OBC是等腰直角三角形,
∴OB2+OC2=BC2,即r2+r2=12,
∴r=
| ||
| 2 |
(2)如图(2)所示,连接OA、OB,过O作OD⊥AB,则AD=
| 1 |
| 2 |
| 1 |
| 2 |
∵△ABC是等边三角形,
∴∠AOB=2∠ACB=2×60°=120°,
∵OD⊥AB,
∴∠AOD=60°,∠OAC=30°,
∴OA=r=
| AD |
| cos∠OAD |
| ||||
|
| ||
| 3 |
(3)如图(3)所示,连接OA、OE,则OE=r,
∵四边形ABCD是正方形,
∴∠OAE=∠AOE=45°,
∴OE=AE=1,
∴AB=2;

(4)如图(4),连接OB,OD,
∵O是切点,
∴OD⊥BC,OD=1,BD=
| a |
| 2 |
∵O是△ABC的内心,
∴∠OBD=30°,
∴OD=BD•tan∠OBD=
| a |
| 2 |
| ||
| 3 |
∴a=2
| 3 |
故答案为:
| ||
| 2 |
| ||
| 3 |
| 3 |
点评:本题考查的是正多边形和圆,解答此类题目的关键是画出图形,利用数形结合求解.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
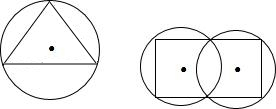
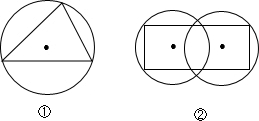
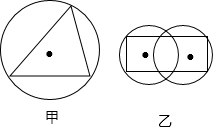
 (2013•嘉定区一模)对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称圆形A被这个圆“覆盖”.例如图中的三角形被一个圆“覆盖”.如果边长为1的正六边形被一个半径长为R的圆“覆盖”,那么R的取值范围为
(2013•嘉定区一模)对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离都不大于这个圆的半径,则称圆形A被这个圆“覆盖”.例如图中的三角形被一个圆“覆盖”.如果边长为1的正六边形被一个半径长为R的圆“覆盖”,那么R的取值范围为