Question

阅读并填充理由（不完整的补充完整）：
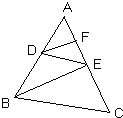
如图所示，已知：DE∥BC，DF、BE分别平分∠ADE和∠ABC，试说明∠FDE=∠DEB．
解：∵DE∥BC________，
∴∠ADE=________，
∵DF、BE分别平分∠ADE和∠ABC（已知），
∴∠ADF=________，∠ABE=________，
∴∠ADF=∠ABE，
∴________∥________，
∴∠FDE=________．

Answer 1

（已知）    ∠ABC    ∠ADE    ∠ABC    DF    BE    ∠DEB
分析：根据平行线的性质与判定，结合角平分线的定义作答．
解答：∵DE∥BC（已知），
∴∠ADE=∠ABC（两直线平行，同位角相等）．
∵DF、BE分别平分∠ADE和∠ABC，
∴∠ADF=∠ADE，∠ABE=∠ABC，
∵∠ADF=∠ABE （同位角相等，两直线平行），
∴DF∥BE（同位角相等，两直线平行），
∴∠FDE=∠DEB（两直线平行，内错角相等）．
故答案为：（已知），∠ABC，∠ADE，∠ABC，DF，DF，∠DEB．
点评：本题考查平行线的判定与性质，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键．