题目内容
 将一副三角板按如图方式叠放在一起,两直角顶点重合于点O.
将一副三角板按如图方式叠放在一起,两直角顶点重合于点O.(1)求∠AOD+∠BOC的度数;
(2)当AB的中点E恰好落在CD的中垂线上时,求∠AOC的度数.
考点:线段垂直平分线的性质
专题:
分析:(1)再根据直角三角板的性质可直接得出结论;
(2)连接OE,根据OE是CD的中垂线可知∠COE=45°,再由E是AB的中点可知OE=
AB=AE,故可得出∠AOE=∠A=60°,再根据∠AOC=∠AOE-∠COE即可得出结论.
(2)连接OE,根据OE是CD的中垂线可知∠COE=45°,再由E是AB的中点可知OE=
| 1 |
| 2 |
解答: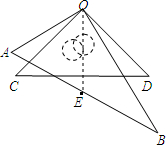 解:(1)∵∠BOC=∠AOB+∠COD-∠AOD,
解:(1)∵∠BOC=∠AOB+∠COD-∠AOD,
∴∠AOD+∠BOC=∠AOB+∠COD=90°+90°=180°;
(2)连接OE,
∵OE是CD的中垂线,
∴∠COE=45°.
又∵E是AB的中点,
∴OE=
AB=AE,.
∴∠AOE=∠A=60°,
∴∠AOC=∠AOE-∠COE=15°.
 解:(1)∵∠BOC=∠AOB+∠COD-∠AOD,
解:(1)∵∠BOC=∠AOB+∠COD-∠AOD,∴∠AOD+∠BOC=∠AOB+∠COD=90°+90°=180°;
(2)连接OE,
∵OE是CD的中垂线,
∴∠COE=45°.
又∵E是AB的中点,
∴OE=
| 1 |
| 2 |
∴∠AOE=∠A=60°,
∴∠AOC=∠AOE-∠COE=15°.
点评:本题考查的是线段垂直平分线的性质,熟知垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.

练习册系列答案
相关题目
 如图,将边长为4cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动三次后,正方形ABCD的中心O所经过的路线长是
如图,将边长为4cm的正方形ABCD沿直线l向右翻动(不滑动),当正方形连续翻动三次后,正方形ABCD的中心O所经过的路线长是 已知:直线l:y=x-2
已知:直线l:y=x-2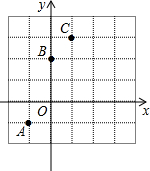 如图,已知二次函数y=ax2+bx+2的图象经过A(-1,-1),C(1,3).
如图,已知二次函数y=ax2+bx+2的图象经过A(-1,-1),C(1,3). 如图,在⊙O中,半径OC⊥弦AB,垂足为D,AB=8,CD=2,求○O的半径.
如图,在⊙O中,半径OC⊥弦AB,垂足为D,AB=8,CD=2,求○O的半径.